Question

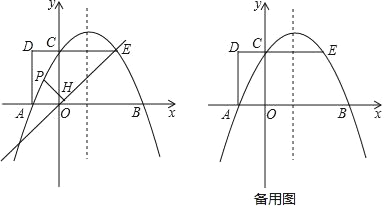
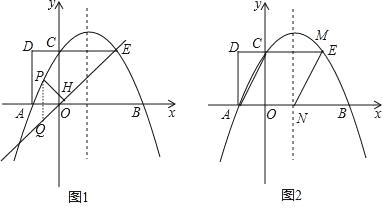
【题目】如图1，抛物线y=ax2+bx+2 与x轴交于A，B两点，与y轴交于点C，AB=4．矩形OADC的边CD=1，延长DC交抛物线于点E．

（1）求抛物线的表达式；

（2）点P是直线EO 上方抛物线上的一个动点，作PH⊥EO，垂足为H，求PH的最大值；

（3）点M在抛物线上，点N在抛物线的对称轴上，若四边形ACMN是平行四边形，求点M、N的坐标．

Answer 1

【答案】（1）抛物线解析式为y=﹣x2+x+2；（2）当x=时，PH的值最大，最大值为；（3）N（1，0）．

【解析】分析：（1）利用矩形的性质和AB＝4确定A（－1，0），B（3，0），然后利用待定系数法求抛物线解析式；

（2）先确定抛物线的对称轴为直线x＝1，C（0，2），利用对称性确定E（2，2），则可得到△OCE为等腰直角三角形，所以∠COE＝45°，作PQ∥y轴交直线OE于Q，如图1，接着判断△PQH为等腰直角三角形得到PH＝PQ，易得直线OE的解析式为y＝x，设P（x，x2＋x＋2），则Q（x，x），所以PQ＝x2＋x＋2，则PH＝(x2＋x＋2)，然后利用二次函数的性质解决问题；

（3）利用平行四边形的性质和点平移的规律得到点C向右平移2个单位可得到M点，则M点的横坐标为2，从而可计算出M点的坐标，然后判断CM∥x轴得到点N为对称轴与x轴的交点，于是得到N点坐标．

详解：（1）∵矩形OADC的边CD＝1，

∴OA＝1，

而AB＝4，

∴OB＝3，

∴A（﹣1，0），B（3，0），

抛物线的解析式为y＝a(x＋1)(x﹣3)，即y＝ax2﹣2ax﹣3a，

∴﹣3a＝2，解得a＝，

∴抛物线解析式为y＝x2＋x＋2；

（2）抛物线的对称轴为直线x＝1，

当x＝0时，y＝x2＋x＋2＝2，则C（0，2），

∵EC∥x轴，

∴点E与点C关于直线x＝1对称，

∴E（2，2），

∵OC＝CE，

∴△OCE为等腰直角三角形，

∴∠COE＝45°，

作PQ∥y轴交直线OE于Q，如图1，

∴∠PGH＝45°，

∵PH⊥OE，

∴△PQH为等腰直角三角形，

∴PH＝PQ，

易得直线OE的解析式为y＝x，

设P（x，x2＋x＋2），则Q（x，x），

∴PQ＝x2＋x＋2－x＝x2＋x＋2，

∴PH＝(x2＋x＋2)

＝x2＋x＋

＝(x﹣)2＋，

当x＝时，PH的值最大，最大值为；

（3）∵四边形ACMN是平行四边形，点A的横坐标为－1，点N的横坐标为1，

∴点A向右平移2个单位可得到N点，

∴点C向右平移2个单位可得到M点，

则M点的横坐标为2，

当x＝2时，y＝x2＋x＋2＝2，则M（2，2），

∴CM∥x轴，

∴点N为对称轴与x轴的交点，

∴N（1，0）．