题目内容
【题目】已知![]() 是一个直角,作射线
是一个直角,作射线![]() ,再分别作
,再分别作![]() 和
和![]() 的平分线
的平分线![]() ,
,![]() .
.
(1)如图①,当![]() 时,求
时,求![]() 的度数;
的度数;
(2)如图②,当射线![]() 在
在![]() 内绕
内绕![]() 点旋转时,
点旋转时,![]() 始终是
始终是![]() 与
与![]() 的平分线.则
的平分线.则![]() 的大小是否发生变化,说明理由;
的大小是否发生变化,说明理由;
(3)当射线![]() 在
在![]() 外绕
外绕![]() 点旋转且
点旋转且![]() 为钝角时,
为钝角时,![]() 仍始终是
仍始终是![]() 与
与![]() 的平分线,直接写出
的平分线,直接写出![]() 的度数(不必写过程).
的度数(不必写过程).

【答案】(1)45°;(2)![]() 的大小不变,见详解;(3)
的大小不变,见详解;(3)![]() 的大小分别为45°和135°
的大小分别为45°和135°
【解析】
(1)根据角平分线的定义可求∠DOE的度数.
(2) )结合角的特点∠DOE=∠DOC+∠COE,求得结果进行判断即可;
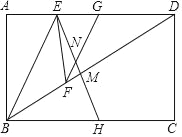
(3)分两种情况考虑,如图3,则∠DOE为45°;如图4,则∠DOE为135°.
解:(1)如图,![]() ,
,
∵![]() 分别平分
分别平分![]() 和
和![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ;
;
(2)![]() 的大小不变,
的大小不变,
理由是:![]()
![]()
![]()
![]()
![]() ;
;
(3)![]() 的大小分别为45°和135°,
的大小分别为45°和135°,
如图3,
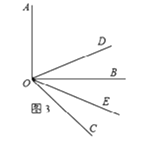
∵OD、OE分别平分∠AOC和∠BOC,
∴∠COD=![]() ∠AOC,∠COE=
∠AOC,∠COE=![]() ∠BOC,
∠BOC,
∴∠DOE=∠COD∠COE=![]() (∠AOC∠BOC)=45°,
(∠AOC∠BOC)=45°,
则![]() 为45°;
为45°;
如图4,
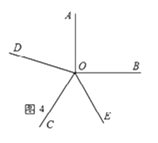
∵OD
∴∠COD=![]() ∠AOC,∠COE=
∠AOC,∠COE=![]() ∠BOC,
∠BOC,
∴∠DOE=∠COD+∠COE=![]() (∠AOC+∠BOC)=
(∠AOC+∠BOC)= ![]() ×270°=135°
×270°=135°
则![]() 为135°.
为135°.
∴![]() 的大小分别为45°和135°
的大小分别为45°和135°

 期末集结号系列答案
期末集结号系列答案【题目】某校在八年级举行“汉字听写”比赛,每位学生听写汉字39个,比赛结束后随机抽查30名学生的听写汉字的正确字数如下:
2 | 9 | 17 | 24 | 33 | 5 | 12 | 19 | 26 | 34 |
7 | 14 | 20 | 26 | 36 | 15 | 22 | 26 | 39 | 31 |
22 | 27 | 39 | 22 | 28 | 23 | 23 | 31 | 30 | 28 |
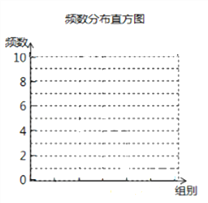
对这30个数据按组距8进行分组,并统计整理.
(1)请完成下面频数分布统计表;
组别 | 正确字数x | 频数 |
A | 0≤x<8 | |
B | 8≤x<16 | |
C | 16≤x<24 | |
D | 24≤x<32 | |
E | 32≤x<40 |
(2)在上图中请画出频数分布直方图;
(3)若该校八年级学生共有1200人,如果听写正确的个数少于24个定为不合格,请你估计该校八年级本次比赛听写不合格的学生人数.