Question

【题目】如图，过正方形ABCD的顶点D作DE∥AC交BC的延长线于点E．

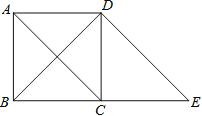
（1）判断四边形ACED的形状，并说明理由；

（2）若BD=8cm，求线段BE的长．

Answer 1

【答案】（1）四边形ACED是平行四边形。理由如下见解析

（2）8cm．

【解析】

试题分析：（1）根据正方形的对边互相平行可得AD∥BC，即为AD∥CE，然后根据两组对边互相平行的四边形是平行四边形解答。

（2）根据正方形的四条边都相等，平行四边形的对边相等可得BC=AD=CE，再根据正方形的边长等于对角线的倍求出BC，然后求出BE即可。

解：（1）四边形ACED是平行四边形。理由如下：

∵四边形ABCD是正方形，∴AD∥BC，即AD∥CE。

∵DE∥AC，∴四边形ACED是平行四边形。

（2）由（1）知，BC=AD=CE=CD，

∵BD=8cm，∴BC=BD=×8=4cm，

∴BE=BC+CE=4+4=8cm．