��Ŀ����
����Ŀ����ͼ����֪l1��l2 �� ��O��l1 �� l2�����У���O�İ뾶Ϊ2cm������ABCD�ı�AD��AB�ֱ���l1 �� l2�غϣ�AB=4 ![]() cm��AD=4cm������O�����ABCD��l1ͬʱ�����ƶ�����O���ƶ��ٶ�Ϊ3cm/s������ABCD���ƶ��ٶ�Ϊ4cm/s�����ƶ�ʱ��Ϊt��s����
cm��AD=4cm������O�����ABCD��l1ͬʱ�����ƶ�����O���ƶ��ٶ�Ϊ3cm/s������ABCD���ƶ��ٶ�Ϊ4cm/s�����ƶ�ʱ��Ϊt��s���� 
��1����ͼ�ڣ�����ͼ���ƶ�һ��ʱ���O�����O1��λ�ã�����ABCD����A1B1C1D1��λ�ã���ʱ��O1 �� A1 �� C1ǡ����ͬһֱ���ϣ����ƶ�ʱ��t= ��
��2�����ƶ������У�Բ��O�����ζԽ���AC����ֱ�ߵľ����ڲ��ϱ仯����þ���Ϊd��cm������d��2ʱ����t��ȡֵ��Χ ��
���𰸡�
��1��2+ ![]()
��2��2�� ![]()
![]() ��t��2+2
��t��2+2 ![]()
���������⣺��1.������OO1 �� ���ӳ���l2�ڵ�E����ͼ1�� 
����O1��O1F��l1�ڵ�F��
��������֪��OO1=3t��AA1=4t��
��tan��DAC= ![]() ��
��
���DAC=60�㣬
��tan��O1A1F= ![]() ��
��
��A1F= ![]()
![]() ��
��
��AA1��A1F=O1E��
��4t�� ![]()
![]() =3t+2��
=3t+2��
��t=2+ ![]() ��
��
��2.����d=2ʱ��
��ʱ��O��ֱ��AC���У�
��ֱ��AC�ڡ�O����ߣ���ͼ2��
�ɣ�1����֪��A1F= ![]()
![]() ��
��
��AA1+A1F=O1E��
��4t+ ![]()
![]() =3t+2��
=3t+2��
��t=2�� ![]()
![]() ��
��
��ֱ��AC�ڡ�O���ұߣ���ͼ3��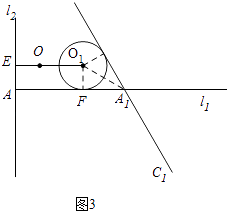
��ʱ��A1F=2 ![]()
��AA1��A1F=O1E��
��4t��2 ![]() =3t+2��
=3t+2��
��t=2+2 ![]() ��
��
������������d��2ʱ��t��ȡֵ��ΧΪ��2�� ![]()
![]() ��t��2+2
��t��2+2 ![]() ��
��
���Դ��ǣ���1��2+ ![]() ����2��2��
����2��2�� ![]()
![]() ��t��2+2
��t��2+2 ![]() ��
��