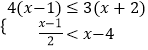题目内容
【题目】填空，完成下面题目的解答，如图，直线AB、CD被直线EF所截，H为CD与EF的交点，∠1=
，∠2=
，GH⊥CD，垂足为H．
解：因为GH⊥CD（已知），
所以∠2+∠3= （垂直的定义）．
因为∠2=（已知），
所以∠3=
=．
所以∠3=∠4=（ ），
又因为∠1=（已知），
所以∠1=∠4，
所以AB∥ （ ）．
【答案】90°对顶角相等，CD，同位角相等，两直线平行
【解析】
要证AB∥CD，只需证∠1=∠4，由已知条件结合垂线定义和对顶角性质，易得∠4=60°，故本题得证．
解：因为GH⊥CD（已知），
所以∠2+∠3= 90° （垂直的定义）．
因为∠2=
（已知），
所以∠3=
=
．
所以∠3=∠4=（ 对顶角相等 ），
又因为∠1=（已知），
所以∠1=∠4，
所以AB∥ CD （同位角相等，两直线平行）．
故答案为：90°，对顶角相等，CD，同位角相等，两直线平行.
练习册系列答案
相关题目
【题目】如图所示，为厉行节能减排，倡导绿色出行，某公司拟在我市甲、乙两个街道社区投放一批共享单车（俗称“小黄车”），这批自行车包括A、B两种不同款型．
成本单价 （单位：元） | 投放数量 （单位：辆） | 总价（单位：元） | |
A型 | x | 50 | 50x |
B型 | x+10 | 50 |
|
成本合计（单位：元） | 7500 | ||
问题1：看表填空
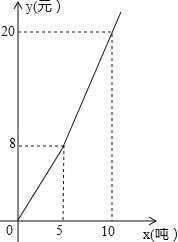
如图2所示，本次试点投放的A、B型“小黄车”共有 辆；用含有x的式子表示出B型自行车的成本总价为 ；
问题2：自行车单价
试求A、B两型自行车的单价各是多少？
问题3：投放数量
现在该公司采取如下方式投放A型“小黄车”：甲街区每100人投放n辆，乙街区每100人投放（n+2）辆，按照这种投放方式，甲街区共投放1500辆，乙街区共投放1200辆，如果两个街区共有
人，求甲街区每100人投放A型“小黄车”的数量．
