题目内容
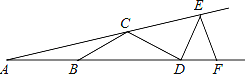
【题目】如图,AB是⊙O的直径,D为⊙O上一点,过 ![]() 上一点T作⊙O的切线TC,且TC⊥AD于点C.
上一点T作⊙O的切线TC,且TC⊥AD于点C. 
(1)若∠DAB=50°,求∠ATC的度数;
(2)若⊙O半径为2,CT= ![]() ,求AD的长.
,求AD的长.
【答案】
(1)解:连接OT,如图1:

∵TC⊥AD,⊙O的切线TC,
∴∠ACT=∠OTC=90°,
∴∠CAT+∠CTA=∠CTA+∠ATO,
∴∠CAT=∠ATO,
∵OA=OT,
∴∠OAT=∠ATO,
∴∠DAB=2∠CAT=50°,
∴∠CAT=25°,
∴∠ATC=90°﹣25°=65°
(2)解:过O作OE⊥AC于E,连接OT、OD,如图2:

∵AC⊥CT,CT切⊙O于T,
∴∠OEC=∠ECT=∠OTC=90°,
∴四边形OECT是矩形,
∴OT=CE=OD=2,
∵OE⊥AC,OE过圆心O,
∴AE=DE= ![]() AD,
AD,
∵CT=OE= ![]() ,
,
在Rt△OED中,由勾股定理得:ED= ![]() ,
,
∴AD=2
【解析】(1)连接OT,根据同角的余角相等得出∠CAD=∠ATO,进而得出∠DAB=2CAT,解答即可;(2)过O作OE⊥AC于E,连接OT、OD,得出矩形OECT,求出OT=CE,根据垂径定理求出DE,根据矩形性质求出OT=CT,根据勾股定理求出即可.
【考点精析】本题主要考查了切线的性质定理的相关知识点,需要掌握切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径才能正确解答此题.

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案
相关题目