题目内容
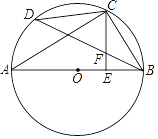
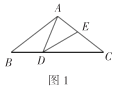
【题目】如图1,在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 是
是![]() 边上的一个动点(不与
边上的一个动点(不与![]() ,
,![]() 重合),以
重合),以![]() 为边作
为边作![]() ,交
,交![]() 边于点
边于点![]() .设
.设![]() ,
,![]() .今天我们将根据学习函数的经验,研究函数值
.今天我们将根据学习函数的经验,研究函数值![]() 随自变量
随自变量![]() 的变化而变化的规律.
的变化而变化的规律.
下面是某同学做的一部分研究结果,请你一起参与解答:
(1)自变量![]() 的取值范围是 ;
的取值范围是 ;
(2)通过计算,得到![]() 与
与![]() 的几组值,如下表:
的几组值,如下表:
| 0.5 | 1 | 1.5 | 2 | 3 | 4 | 4.5 | 5 | 5.5 |
| 3.3125 | 2.75 | 2.3125 | 2 | 2.3125 | 2.75 | 3.3125 |
请你补全表格;
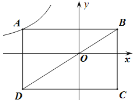
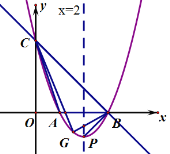
(3)在如图2所示的平面直角坐标系中,画出该函数的大致图象;
(4)根据图象,请写出该函数的一条性质.
【答案】(1)![]() (2)1.75;2 (3)见解析 (4)当
(2)1.75;2 (3)见解析 (4)当![]() 时,
时,![]() 随
随![]() 的增大而减小;当
的增大而减小;当![]() 时,
时,![]() 随
随![]() 的增大而增大.
的增大而增大.
【解析】
(1)根据题意,直接写出x的取值范围,即可;
(2)先证BAD~CDE,可得![]() ,进而得y关于x的解析式,分别求出当x=3时,当x=4时,y的值,即可;
,进而得y关于x的解析式,分别求出当x=3时,当x=4时,y的值,即可;
(3)根据函数解析式或表格中的数据与自变量的取值范围,画出函数图象,即可;
(4)根据二次函数的性质,即可得到答案.
(1)∵点![]() 是
是![]() 边上的一个动点(不与
边上的一个动点(不与![]() ,
,![]() 重合),
重合),![]() ,
,
∴![]() ,
,
故答案是:![]() ;
;
(2)∵∠B+∠BAD=∠ADE+∠CDE,![]() ,
,
∴∠BAD=∠CDE,
∵![]() ,
,
∴∠B=∠C,
∴BAD~CDE,
∴![]() ,即:
,即:![]() ,
,
∴![]() ,
,
∴当x=3时,y=1.75;当x=4时,y=2,
故答案是:1.75,2;
(3)函数图象如下:
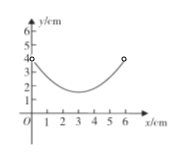
(4)由函数的图象和性质可知:当![]() 时,
时,![]() 随
随![]() 的增大而减小;当
的增大而减小;当![]() 时,
时,![]() 随
随![]() 的增大而增大.
的增大而增大.

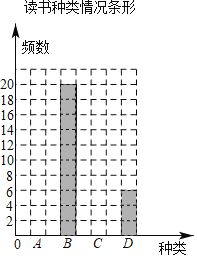
【题目】寒假中,某校七年级开展“阅读经典,读一本好书”的活动.为了解学生阅读情况,从全年级学生中随机抽取了部分学生调查读书种类情况,并进行统计分析,绘制了如下不完整的统计图表:
读书种类情况统计表
种类 | 频数 | 百分比 |
A.科普类 | a | 32% |
B.文学类 | 20 | 40% |
C.艺术类 | 8 | b |
D.其他类 | 6 | 12% |
请根据以上信息,解答下列问题:
(1)填空:a= ,b= ,并补全条形统计图;
(2)若绘制“阅读情况扇形统计图”,则“艺术类”所对应扇形的圆心角度数为 °;
(3)若该校七年级共有800人,请估计全年级在本次活动中读书种类为“艺术类”的学生人数.