题目内容
【题目】如图, AB 是 ⊙ O 的直径, C 是![]() 的中点, CE ⊥ AB 于 E , BD 交 CE 于 F .
的中点, CE ⊥ AB 于 E , BD 交 CE 于 F .
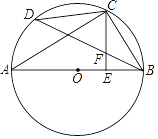
(1)求证: CF=BF ;
(2)若 CD=6 ,AC=8 ,求 BE 、 CF 的长.
【答案】(1)见解析;(2)3.6 ,![]()
【解析】
(1)延长CE交⊙O于点 P,根据垂径定理得出及圆周角定理得出 ∠BCP=∠BDC ,又由C 是![]() 的中点,得∠BDC=∠CBD ,进而得出∠CBD=∠BCP ,从而得出结论;
的中点,得∠BDC=∠CBD ,进而得出∠CBD=∠BCP ,从而得出结论;
(2)根据圆周角定理及勾股定理得出 AB 的长,再由直角三角形相似,推出对应边成比例,得出 BE 及 CE 的长,设 CF=x ,则 FE=4.8﹣x , BF=x ,根据勾股定理得出方程求解即可.
(1)证明:延长 CE 交 ⊙ O 于点 P ,
∵ CE ⊥ AB ,∴![]() ,
,
∴∠ BCP= ∠ BDC ,
∵ C 是![]() 的中点,
的中点,
∴ CD=CB ,
∴∠ BDC= ∠ CBD ,
∴∠ CBD= ∠ BCP ,
∴ CF=BF ;
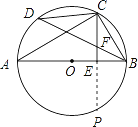
(2) ∵ CD=6 , AC=8 ,
∴ AB=10 ,
∵CF⊥AB,AC⊥BC, ∠CBA=∠EBC
∴△CBA∽△EBC
∴![]()
∴ BE= ![]() =3.6 ,
=3.6 ,
同理![]()
∴![]()
∴![]()
设 CF=x ,则 FE=4.8- x , BF=x ,
∵EF2+BE2=BF2
∴ (4.8﹣x)2 +3.62 =x2 ,
∴ x= ![]()
∴ CF=![]() .
.

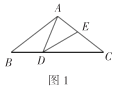
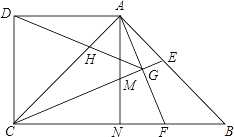
【题目】如图1,在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 是
是![]() 边上的一个动点(不与
边上的一个动点(不与![]() ,
,![]() 重合),以
重合),以![]() 为边作
为边作![]() ,交
,交![]() 边于点
边于点![]() .设
.设![]() ,
,![]() .今天我们将根据学习函数的经验,研究函数值
.今天我们将根据学习函数的经验,研究函数值![]() 随自变量
随自变量![]() 的变化而变化的规律.
的变化而变化的规律.
下面是某同学做的一部分研究结果,请你一起参与解答:
(1)自变量![]() 的取值范围是 ;
的取值范围是 ;
(2)通过计算,得到![]() 与
与![]() 的几组值,如下表:
的几组值,如下表:
| 0.5 | 1 | 1.5 | 2 | 3 | 4 | 4.5 | 5 | 5.5 |
| 3.3125 | 2.75 | 2.3125 | 2 | 2.3125 | 2.75 | 3.3125 |
请你补全表格;
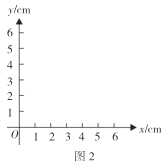
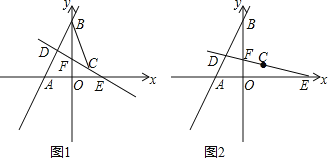
(3)在如图2所示的平面直角坐标系中,画出该函数的大致图象;
(4)根据图象,请写出该函数的一条性质.