题目内容
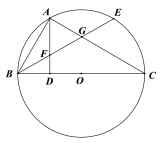
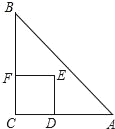
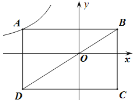
【题目】如图,在平面直角坐标系中,矩形ABCD的对角线BD经过坐标原点O,矩形的边分别平行于坐标轴,点A在函数![]() (
(![]() ≠0,
≠0,![]() <0)的图象上,点C的坐标为(2,
<0)的图象上,点C的坐标为(2,![]() ),则
),则![]() 的值为( )
的值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】D
【解析】
根据反比例函数的几何意义只要求出矩形OGAH的面积也可,依据矩形的性质发现S矩形OGAH=S矩形OECF,而S矩形OECF可通过点C(2,![]() )转化为线段长而求得,再根据反比例函数的所在的象限,确定k的值即可.
)转化为线段长而求得,再根据反比例函数的所在的象限,确定k的值即可.
解:如图,根据矩形的性质可得:S矩形OGAH=S矩形OECF,
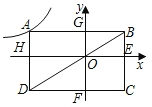
∵点C的坐标为(2,-2),
∴OE=2,OF=2,
∴S矩形OECF=OEOF=4,
设A(a,b),则OH=-a,OG=b,
∴S矩形OGAH=OHOG=-ab=4,
又∵点A在函数![]() (k≠0,x<0)的图象上,
(k≠0,x<0)的图象上,
∴![]() ;
;
故选:D.

练习册系列答案
相关题目
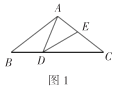
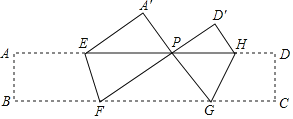
【题目】如图1,在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 是
是![]() 边上的一个动点(不与
边上的一个动点(不与![]() ,
,![]() 重合),以
重合),以![]() 为边作
为边作![]() ,交
,交![]() 边于点
边于点![]() .设
.设![]() ,
,![]() .今天我们将根据学习函数的经验,研究函数值
.今天我们将根据学习函数的经验,研究函数值![]() 随自变量
随自变量![]() 的变化而变化的规律.
的变化而变化的规律.
下面是某同学做的一部分研究结果,请你一起参与解答:
(1)自变量![]() 的取值范围是 ;
的取值范围是 ;
(2)通过计算,得到![]() 与
与![]() 的几组值,如下表:
的几组值,如下表:
| 0.5 | 1 | 1.5 | 2 | 3 | 4 | 4.5 | 5 | 5.5 |
| 3.3125 | 2.75 | 2.3125 | 2 | 2.3125 | 2.75 | 3.3125 |
请你补全表格;
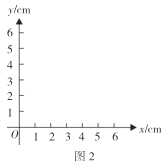
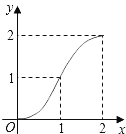
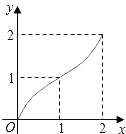
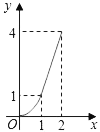
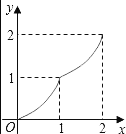
(3)在如图2所示的平面直角坐标系中,画出该函数的大致图象;
(4)根据图象,请写出该函数的一条性质.