题目内容
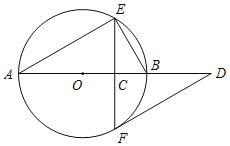
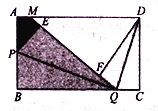
【题目】如图,四边形ABCD是正方形,E,F分别在线段BC和CD上,![]() .连接EF。将△ADF绕着点顺时针旋转90°,得到
.连接EF。将△ADF绕着点顺时针旋转90°,得到![]()
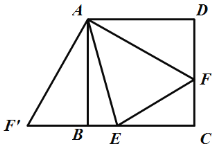
(1)证明:![]()
(2)证明:EF=BE+DF.
(3)已知正方形ABCD边长是6,EF=5,求线段BE的长.
【答案】(1)见解析;(2)见解析(3)2或3
【解析】
(1)由旋转的性质得到![]() ,
,![]() ,
,![]() ,然后得到
,然后得到![]() ,利用SAS证明三角形全等即可;
,利用SAS证明三角形全等即可;
(2)由(1)知DF=BF’,即可得到EF=BE+DF;
(3)设BE=x,则DF=5-x,得到CF=x+1,利用勾股定理得![]() ,即可求出BE的长度.
,即可求出BE的长度.
解:(1)由旋转的性质可得![]() ,
,![]() ,
,![]() 。
。
∵![]() ,
,![]()
∴![]()
∴![]()
∵![]() ,
,![]() ,
,![]()
∴![]() ;
;
(2)∵![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴EF=BE+DF;
(3)∵BE=x,EF=BE+DF ,EF=5,
∴DF=5-x,
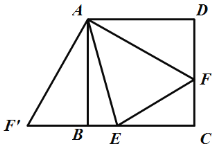
又∵正方形ABCD边长是6,即BC=CD=6,
∴CE=BC-BE=6-x,CF=CD-DF=6-(5-x)=x+1,
在Rt△CEF中,有![]() ,
,
即![]() ,
,
解得:![]() ;
;
∴线段BE的长为2或3.

练习册系列答案
相关题目
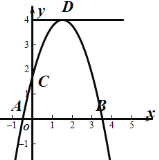
【题目】已知二次函数![]() 的
的![]() 与
与![]() 的部分对应值如表:
的部分对应值如表:
|
| 0 | 2 | 3 | 4 |
| 5 | 0 |
|
| 0 |
下列结论:①抛物线的开口向上;②抛物线的对称轴为直线![]() ;③当
;③当![]() 时,
时,![]() ;④3是方程
;④3是方程![]() 的一个根;⑤若
的一个根;⑤若![]() ,
,![]() 是抛物线上两点,则
是抛物线上两点,则![]() ,其中正确的个数是( )
,其中正确的个数是( )
A.1B.2C.3D.4