题目内容
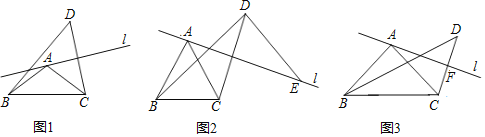
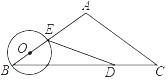
【题目】如图,等腰△ABC中,AB=AC=5cm,BC=8cm.动点D从点C出发,沿线段CB以2cm/s的速度向点B运动,同时动点O从点B出发,沿线段BA以1cm/s的速度向点A运动,当其中一个动点停止运动时另一个动点也随时停止.设运动时间为t(s),以点O为圆心,OB长为半径的⊙O与BA交于另一点E,连接ED.当直线DE与⊙O相切时,t的取值是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】A
【解析】
如图,作AF⊥BC于F,利用等腰三角形的性质得BF=CF=4,利用切线的判定方法,当BE⊥DE,直线DE与![]() 相切,则∠BED=90°,然后利用cos
相切,则∠BED=90°,然后利用cos![]() B =
B =![]() , 可得cos
, 可得cos![]() B =
B =![]() ,可求出t的值.
,可求出t的值.
由题意可知![]() ,过点A作AF⊥BC于点F,
,过点A作AF⊥BC于点F,
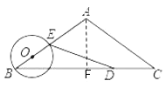
∵AB=AC,
则BF=CF=4cm,
∴cos![]() B=
B=![]() ,
,
当直线DE与⊙O相切时,DE⊥AB,
则cos![]() B =
B =![]() ,
,
即![]() ,解得
,解得![]() .
.
故选A.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目