题目内容
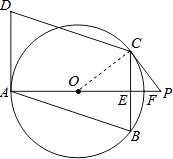
【题目】如图,四边形ABCD是平行四边形,点A、B、C在☉O上,AD与⊙O相切,射线AO交BC于点E,交⊙O于点F.点P在射线AO上,且∠PCB=2∠BAF.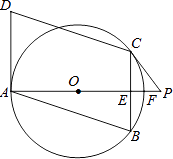
(1)求证:直线PC是⊙O的切线;
(2)若AB= ![]() ,AD=2,求线段PC的长.
,AD=2,求线段PC的长.
【答案】
(1)证明:连接OC,
∵AD与⊙O相切于点A,
∴FA⊥AD,
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴FA⊥BC,
∵FA经过圆心O,
∴F是弧BC的中点,BE=CE,∠OEC=90°,
∴∠COF=2∠BAF.
∵∠PCB=2∠BAF,
∴∠PCB=∠COF,
∵∠OCE+∠COF=180°﹣∠OEC=90°,
∴∠OCE+∠PCB=90°.
∴OC⊥PC,
∵点C在⊙O上,
∴直线PC是⊙O的切线;
(2)解:∵四边形ABCD是平行四边形,
∴BC=AD=2,
∴BE=CE=1,
在Rt△ABE中,∠AEB=90°,AB= ![]() ,
,
∴AE= ![]() ,
,
设⊙O的半径为r,则OC=OA=r,OE=3﹣r,
在Rt△OCE中,∠OEC=90°,
∴OC2=OE2+CE2,
∴r2=(3﹣r)2+1,
解得r= ![]() ,
,
∵∠COE=∠PCE,∠OEC=∠CEP=90°.
∴△OCE∽△CPE,
∴ ![]() .
.
∴ ![]() =
= ![]() ,
,
∴CP= ![]() .
.
【解析】(1)连接OC,首先依据切线的性质可得到FA⊥AD,然后平行线的定义可得到AD∥BC,然后由垂径定理可证得F是弧BC的中点,BE=CE,∠OEC=90°,然后结合条件∠PCB=2∠BAF,可得到∠OCE+∠PCB=90°,最后,再依据切线的判定定理进行证明即可;
(2)依据勾股定理可求得AE的长,设⊙O的半径为r,则OC=OA=r,OE=3-r,在Rt△OCE中,依据勾股定理列出关于r的方程可求得r的值,接下来,再证明△OCE∽△CPE,然后由相似三角形的对应边成比例可求得线段PC的长.
【考点精析】根据题目的已知条件,利用平行四边形的性质和相似三角形的判定与性质的相关知识可以得到问题的答案,需要掌握平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分;相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方.

 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案【题目】为了调查学生对雾霾天气的了解程度,某校在学生中做了一次抽样调查,调查结果共分为四个等级:A.非常了解;B.比较了解;C.基本了解;D.不了解.根据调查统计结果,绘制了如图所示的不完整的三种统计图表.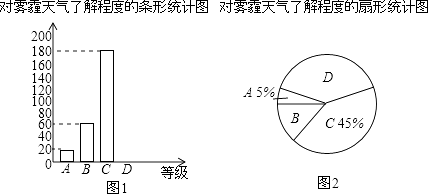
对雾霾的了解程度 | 百分比 |
A.非常了解 | 5% |
A.比较了解 | 15% |
C.基本了解 | 45% |
D.不了解 | n |
请结合统计图表,回答下列问题:
(1)本次参与调查的学生共有人,n=;扇形统计图中D部分扇形所对应的圆心角是度;
(2)请补全条形统计图;
(3)根据调查结果,学校准备开展关于雾霾的知识竞赛,某班要从“非常了解”程度的小明和小刚中选一人参加,现设计了如下游戏来确定,具体规则是:把四个完全相同的乒乓球标上数字1,2,3,4,然后放到一个不透明的袋中,一个人先从袋中随机摸出一个球,另一人再从剩下的三个球中随机摸出一个球.若摸出的两个球上的数字和为奇数,则小明去,否则小刚去.请用树状图或列表法说明这个游戏规则是否公平.