Question

【题目】已知：在中，，．

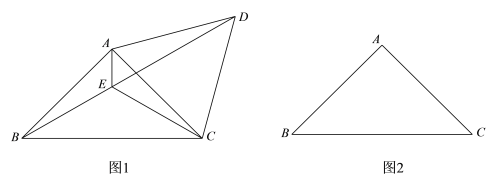
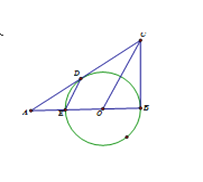
（1）如图1，将线段绕点逆时针旋转得到，连结、，的平分线交于点，连结．

①求证：；②用等式表示线段、、之间的数量关系(直接写出结果)；

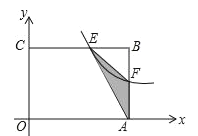
（2）在图2中，若将线段绕点顺时针旋转得到，连结、，的平分线交的延长线于点，连结．请补全图形，并用等式表示线段、、之间的数量关系，并证明．

Answer 1

【答案】（1）①见解析；② 2CE+ AE=BD，(＋ 2 )AE＋EC＝BD 或BD=(AE＋CE )，答案不唯一；（2）见解析，2CE-AE=BD，答案不唯一，见解析.

【解析】

（1）①首先证明△ABE≌△ACE，由旋转的性质，全等的性质和等腰直角三角形的性质求得，然后由三角形外角的性质可求出，问题得证；

②在ED上截取EH=AE，易得△AEH为等边三角形，然后证明△AEB≌△AHD，通过线段间的等量代换即可得到2CE+ AE=BD；

（2）首先根据题意补全图形，以A为顶点，AE为一边作∠EAF=60°，AF交DB延长线于点F，证明△AEF是等边三角形，△CAE≌△DAF（SAS）和△BAE≌△CAE（SAS），然后根据线段和差进行等量代换得到结果.

解：（1）①证明：∵，，平分，

∴，．

又∵ AE=AE，

∴△ABE≌△ACE（SAS）．

∴．

由旋转可得△ACD是等边三角形．

∴，．

∴，．

∴．

∴．

∵，．

∴．

∴．

．

②线段、、之间的数量关系是：2CE+ AE=BD．答案不唯一，如(＋ 2 )AE＋EC＝BD或BD=(AE＋CE )

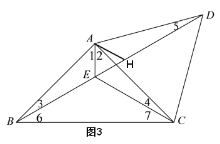
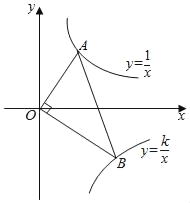
如图3，在ED上截取EH=AE，

∵，

∴△AEH为等边三角形，

∴AE=AH，∠AEH=∠AHE=60°，

∴∠AEB=∠AHD=120°，

又∵，

∴△AEB≌△AHD，

∴BE=DH，

∵BD=BE+EH+DH，BE=CE，AE=EH，

∴BD=CE+AE+CE，

即2CE+ AE=BD.

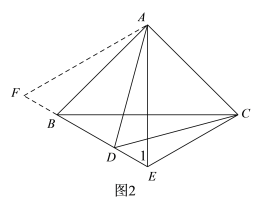
（2）补全图形如图2，

线段、、之间的数量关系是：2CE -AE=BD．（答案不唯一）

证明：如图2，以A为顶点，AE为一边作∠EAF=60°，AF交DB延长线于点F．

∵，，平分，

∴．

由旋转可得△ACD是等边三角形．

∴，．

∴，．

∴．

∴．

∴．

又∵∠EAF=60°，

∴．

∴△AEF是等边三角形．

∴AE=AF=EF．

在△CAE和△DAF中，

∵，，AE=AF，

∴△CAE≌△DAF（SAS）．

∴CE=DF．

∵，，AE=AE，

∴△BAE≌△CAE（SAS）．

∴BE=CE．

∵DF+BE-EF=BD，

∴2CE-AE=BD．