题目内容
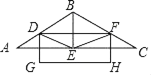
【题目】如图,在边长4的正方形ABCD中,E是边BC的中点,将△CDE沿直线DE折叠后,点C落在点F处,冉将其打开、展平,得折痕DE。连接CF、BF、EF,延长BF交AD于点G。则下列结论:①BG= DE;②CF⊥BG;③sin∠DFG= ![]() ;④S△DFG=
;④S△DFG=![]() .其中正确的有( )
.其中正确的有( )

A. 1个
B. 2个
C. 3个
D. 4个
【答案】C
【解析】
①证明BG∥ED可得平行四边形BEDG即可;
②根据直角三角形斜边上的中线是斜边的一半来求解;
③证明∠DFG=∠FCB即可;
④求出sin∠GFD,用S△DFG=![]() sin∠GFD即可求解.
sin∠GFD即可求解.
①由折叠可得CF⊥DE,EF=CE
∵E是边BC的中点
∴EF=CE=![]()
∴CF⊥BG
∴BG∥ED
∴四边形BEDG是平行四边形
∴BG= DE
②由折叠可得EF=CE
∵E是边BC的中点
∴EF=CE=![]()
∴CF⊥BG
③由折叠可得DE垂直平分CF,∠EFD=90°, ∠EFC =∠FCB
由勾股定理可得DE=![]()
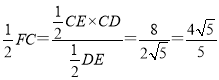 ,FC=
,FC=![]()
BF=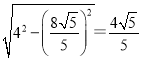
∵CF⊥BG,∠EFD=90°
∴∠CFD+∠GFD=90°, ∠EFC+∠CFD==90°
∴∠EFC=∠GFD=∠FCB
sin∠DFG= sin∠FCB=![]()
∴③错误
④由折叠可得FD=CD
∵BF=![]() ,BG=DE=
,BG=DE=![]()
∴FG=![]()
∴S△DFG=![]() sin∠GFD=
sin∠GFD=![]()

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案
相关题目