Question

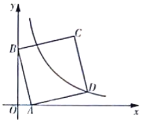
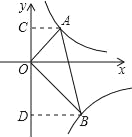
【题目】如图，已知点A、B分别在反比例函数（x＞0），（k＜0，x＞0）的图象上．点B的横坐标为4，且点B在直线y＝x﹣5上．

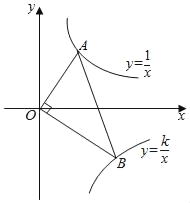
（1）求k的值；（2）若OA⊥OB，求tan∠ABO的值．

Answer 1

【答案】（1）k＝-4；（2）tan∠ABO=．

【解析】

（1）根据一次函数图象上点的坐标特征，求得B点的坐标，然后根据待定系数法即可求得k的值；

（2）过A作AC垂直于y轴，过B作BD垂直于y轴，易证△AOC∽△OBD，利用反比例函数k的几何意义求出两三角形的面积，进一步求得OA与OB的比值，在直角三角形AOB中，利用锐角三角函数定义即可求出tan∠B的值．

解：（1）∵点B的横坐标为4，且点B在直线y＝x﹣5上．

∴点B的纵坐标为y＝4﹣5＝﹣1，

∴B（4，﹣1），

∵B在反比例函数y＝（k＜0，x＞0）的图象上

∴k＝4×（﹣1）＝﹣4；

（2）过A作AC⊥y轴，过B作BD⊥y轴，可得∠ACO＝∠BDO＝90°，

∴∠AOC+∠OAC＝90°，

∵OA⊥OB，

∴∠AOC+∠BOD＝90°，

∴∠OAC＝∠BOD，

∴△AOC∽△OBD，

∵点A、B分别在反比例函数y＝（x＞0），y＝（x＞0）的图象上，

∴S△AOC＝ ，S△OBD＝，

∴S△AOC：S△OBD＝1：|k|，

∴，

∴，

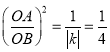则在Rt△AOB中，tan∠ABO＝．