Question

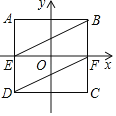
【题目】如图，正方形ABCD的对称中心在坐标原点，AB∥x轴，AD，BC分别与x轴交于E，F，连接BE，DF，若正方形ABCD的顶点B，D在双曲线y＝上，实数a满足a1﹣a＝1，则四边形DEBF的面积是(　　)

A. B. C. 1D. 2

Answer 1

【答案】D

【解析】

依据实数a满足a1﹣a＝1，即可得出a＝1，再根据反比例函数系数k的几何意义以及正方形的性质，即可得到四边形DEBF的面积．

∵实数a满足a1﹣a＝1，

∴a＝±1，

又∵a＞0，

∴a＝1，

∵正方形ABCD的顶点B，D在双曲线y上，

∴S矩形BGOF＝1，

又∵正方形ABCD的对称中心在坐标原点，

∴S平行四边形DEBF＝S矩形ABFEF＝2S矩形BGOF＝2×1＝2，

故选：D．