题目内容
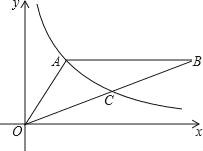
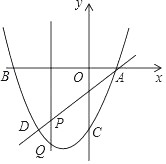
【题目】如图,已知A,B是反比例函数y=![]() (k>0,x>0)图象上的两点,BC∥x轴,交y轴于点C,动点P从坐标原点O出发,沿O→A→B→C(图中“→”所示路线)匀速运动,终点为C,过P作PM⊥x轴,垂足为M.设三角形OMP的面积为S,P点运动时间为r,则S关于t的函数图象大致为( )
(k>0,x>0)图象上的两点,BC∥x轴,交y轴于点C,动点P从坐标原点O出发,沿O→A→B→C(图中“→”所示路线)匀速运动,终点为C,过P作PM⊥x轴,垂足为M.设三角形OMP的面积为S,P点运动时间为r,则S关于t的函数图象大致为( )

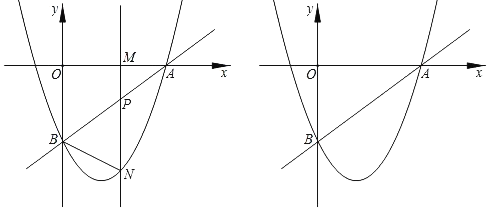
A. 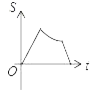 B.
B. 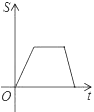 C.
C. 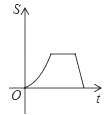 D.
D. 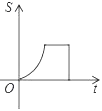
【答案】C
【解析】
结合点P的运动,将点P的运动路线分成O→A、A→B、B→C三段位置来进行分析三角形OMP面积的计算方式,通过图形的特点分析出面积变化的趋势,从而得到答案.
解:设∠AOM=α,点P运动的速度为a,
当点P从点O运动到点A的过程中,
S![]() ,
,
从而可知图象本段应为抛物线,且S随着t的增大而增大;
当点P从A运动到B时,由反比例函数性质可知△OPM的面积为![]() k,保持不变,
k,保持不变,
故本段图象应为与横轴平行的线段;
当点P从B运动到C过程中,OM的长在减少,△OPM的高与在B点时相同,
故本段图象应该为一段下降的线段;
故选:C.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目