题目内容
【题目】下面是小明设计的“作三角形的高线”的尺规作图过程.
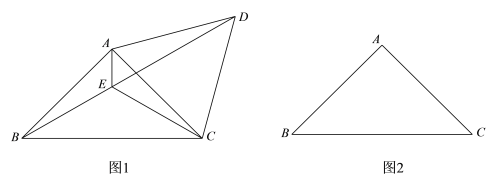
已知：△ABC．
求作：BC边上的高线．
作法：如图，
①分别以A，B为圆心，大于
长为半径画弧，两弧交于点D，E；
②作直线DE，与AB交于点F，以点F为圆心，FA长为半径画圆，交CB的延长线于点G；
③连接AG．
所以线段AG就是所求作的BC边上的高线．
根据小明设计的尺规作图过程，
（1）使用直尺和圆规，补全图形；（保留作图痕迹）
（2）完成下面证明.
证明：连接DA，DB，EA，EB，
∵DA=DB，
∴点D在线段AB的垂直平分线上（ ）（填推理的依据）．
∵ = ，
∴点E在线段AB的垂直平分线上．
∴DE是线段AB的垂直平分线．
∴FA=FB．
∴AB是⊙F的直径．
∴∠AGB=90°（ ）（填推理的依据）．
∴AG⊥BC
即AG就是BC边上的高线．
【答案】（1）见解析；（2）到线段两端距离相等的点在这条线段的垂直平分线上；EA，EB；直径所对的圆周角是直角.
【解析】
（1）根据题中步骤，补全图形即可；
（2）根据作图可知DE是线段AB的垂直平分线，FA=FB，然后根据直径所对的圆周角是直角证明AG是BC边上的高线.
解：（1）使用直尺和圆规，补全图形；（保留作图痕迹）
（2）证明：连接DA，DB，EA，EB，
∵DA=DB，
∴点D在线段AB的垂直平分线上（到线段两端距离相等的点在这条线段的垂直平分线上）（填推理的依据）．
∵EA=EB，
∴点E在线段AB的垂直平分线上．
∴DE是线段AB的垂直平分线．
∴FA=FB．
∴AB是⊙F的直径．
∴∠AGB=90°（直径所对的圆周角是直角）（填推理的依据）．
∴AG⊥BC
即AG就是BC边上的高线．
练习册系列答案
相关题目
