Question

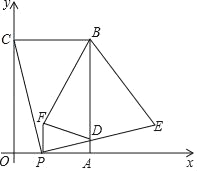
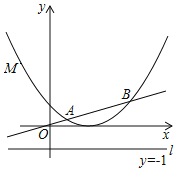
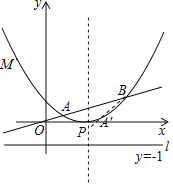
【题目】在平面直角坐标系xOy中，已知抛物线的顶点坐标为（2，0），且经过点（4，1），如图，直线y＝x与抛物线交于A、B两点，直线l为y＝﹣1．

（1）求抛物线的解析式；

（2）在抛物线的对称轴上是否存在一点P，使|PA﹣PB|取得最大值？若存在，求出点P的坐标；若不存在，请说明理由；

（3）已知F（x0，y0）为平面内一定点，M（m，n）为抛物线上一动点，且点M到直线l的距离与点M到点F的距离总是相等，求定点F的坐标．

Answer 1

【答案】（1）y＝（x﹣2）2；（2）P（2，﹣）；（3）F（2，1）.

【解析】

（1）设函数解析式为y＝a（x﹣2）2，将点（4，1）代入，即可求解析式；

（2）联立方程求出对称轴x＝2，点A关于对称轴的对称点为 当点P，A'，B共线时，|PA﹣PB|取得最大值；待定系数法求出直线A'B的解析式即可求点P；

（3）由 点M到直线l的距离与点M到点F的距离总是相等，得到将代入，整理得到由m是任意的，所以有方程组，求解即可．

解：（1）设函数解析式为y＝a（x﹣2）2，

将点（4，1）代入，

得到a＝，

∴

（2）与的交点

对称轴x＝2，

点A关于对称轴的对称点为

当点P，A'，B共线时，|PA﹣PB|取得最大值；

设直线A'B的解析式为y＝kx+b，

∴

∴

∴

∴

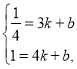
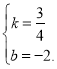
（3）∵点M到直线l的距离与点M到点F的距离总是相等，

∴

∴

∵,

∴

∴

∴

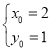
∴F（2，1）；