题目内容
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 在斜边
在斜边![]() 上,连接
上,连接![]() ,把
,把![]() 沿直线
沿直线![]() 翻折,使点
翻折,使点![]() 落在同一平面内的点
落在同一平面内的点![]() 处.当
处.当![]() 与
与![]() 的直角边垂直时,
的直角边垂直时,![]() 的长为__________.
的长为__________.

【答案】1或![]()
【解析】
分两种情况讨论,当A′D⊥AC时,易证A′D∥BC,A′C⊥AB,△BCH∽△BAC,求得CH和A′H的长,再证得△A′HD∽△CHB,,求得A′D=1,即AD=1;当A′D⊥BC时,则A′D∥AC,AD=A′D,AC=A′C,∠ACD=∠A′CD,推出∠A′DC=∠A′CD,则A′D=A′C,即可求得答案.
在Rt△ABC中,AB=4,BC=3,
∴![]() ,
,
如图,当A′D⊥AC,
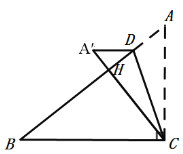
∵把△ACD沿直线CD折叠,点A落在同一平面内的A′处,
∴∠A′=∠A,A′D=AD,A′C=AC,
∵BC⊥AC,
∴A′D∥BC,
∠A′=∠A′CB =∠A,
∵∠B=∠B,
∴△BCH∽△BAC,
∴![]() ,即
,即![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵A′D∥BC,
∴△A′HD∽△CHB,
∴![]() ,即
,即 ,
,
解得:A′D=1,
∴AD=1;
如图,当A′D⊥BC时,则A′D∥AC,
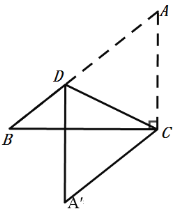
∵把△ACD沿直线CD折叠,点A落在同一平面内的A′处,
∴AD=A′D,AC=A′C,∠ACD=∠A′CD,
∵A′D∥AC,
∴∠A′DC=∠ACD,
∴∠A′DC=∠A′CD,
∴A′D=A′C,
∴AD=AC=![]() ,
,
综上所述:AD的长为:1或![]() ,
,
故答案为:1或![]() .
.

练习册系列答案
相关题目