题目内容
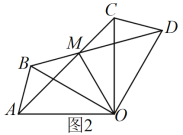
【题目】在△ABC中,∠BAC=90°,AB=AC,D为△ABC外一点,且AD=AC,则∠BDC的度数为__________.
【答案】45°或135°
【解析】试题分析:以点A为圆心作圆,点D即为其圆上的点,B、C点除外,因此∠BDC的度数分为两种情况,即点D在弧BC的优弧上时和劣弧上时,根据等腰直角三角形以及圆心角和圆周角的概念,可求出∠BDC的度数为45°或135°.
解:∵在△ABC中,∠BAC=90°,AB=AC,D为△ABC形外一点,且AD=AC,
∴点D是以点A为圆心的圆上的点,B、C除外.
∴如图所示,当点D在优弧BC上时∠BDC=45°;当点D在劣弧BC上时∠BDC=135°(点D在D1位置时).
故答案为45°或135°.


练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
【题目】为了从甲、乙两人中选拔一人参加射击比赛,现对他们的射击成绩进行了测试,5次打靶命中的环数如下:
甲:8,7,9,8,8; 乙:9,6,10,8,7;
(1)将下表填写完整:
平均数 | 中位数 | 方差 | |
甲 | 8 | ||
乙 | 8 | 2 |
(2)根据以上信息,若你是教练,你会选择谁参加射击比赛,理由是什么?
(3)若乙再射击一次,命中8环,则乙这六次射击成绩的方差会 .(填“变大”或“变小”或“不变”)