题目内容
【题目】如图,在矩形ABCD中,AB=8,BC=16,将矩形ABCD沿EF折叠,使点C与点A重合,则折痕EF的长为( )

A.6 B.12 C.2![]() D.4
D.4![]()
【答案】D.
【解析】
试题解析:设BE=x,则CE=BC-BE=16-x,
∵沿EF翻折后点C与点A重合,
∴AE=CE=16-x,
在Rt△ABE中,AB2+BE2=AE2,
即82+x2=(16-x)2,
解得x=6,
∴AE=16-6=10,
由翻折的性质得,∠AEF=∠CEF,
∵矩形ABCD的对边AD∥BC,
∴∠AFE=∠CEF,
∴∠AEF=∠AFE,
∴AE=AF=10,
过点E作EH⊥AD于H,则四边形ABEH是矩形,
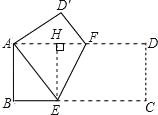
∴EH=AB=8,
AH=BE=6,
∴FH=AF-AH=10-6=4,
在Rt△EFH中,EF=![]() .
.
故选D.

练习册系列答案
相关题目