题目内容
如图①,若二次函数 的图象与x轴交于点A(-2,0),B(3,0)两点,点A关于正比例函数
的图象与x轴交于点A(-2,0),B(3,0)两点,点A关于正比例函数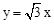 的图象的对称点为C。
的图象的对称点为C。
(1)求b、c的值;
(2)证明:点C 在所求的二次函数的图象上;
(3)如图②,过点B作DB⊥x轴交正比例函数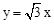 的图象于点D,连结AC,交正比例函数
的图象于点D,连结AC,交正比例函数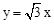 的图象于点E,连结AD、CD。如果动点P从点A沿线段AD方向以每秒2个单位的速度向点D运动,同时动点Q从点D沿线段DC方向以每秒1个单位的速度向点C运动,当其中一个到达终点时,另一个随之停止运动,连结PQ、QE、PE,设运动时间为t秒,是否存在某一时刻,使PE平分∠APQ,同时QE平分∠PQC,若存在,求出t的值;若不存在,请说明理由。
的图象于点E,连结AD、CD。如果动点P从点A沿线段AD方向以每秒2个单位的速度向点D运动,同时动点Q从点D沿线段DC方向以每秒1个单位的速度向点C运动,当其中一个到达终点时,另一个随之停止运动,连结PQ、QE、PE,设运动时间为t秒,是否存在某一时刻,使PE平分∠APQ,同时QE平分∠PQC,若存在,求出t的值;若不存在,请说明理由。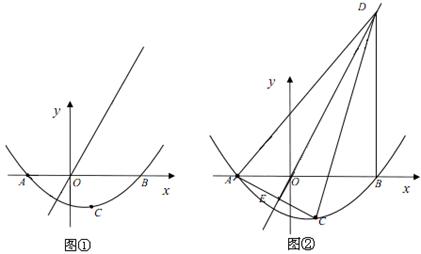
(1)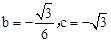 。
。
(2)利用轴对称和锐角三角函数求出点C的坐标,代入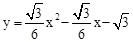 验证即可。
验证即可。
(3)存在时刻 ,使PE平分∠APQ,同时QE平分∠PQC。
,使PE平分∠APQ,同时QE平分∠PQC。
解析分析:(1)将A(-2,0),B(3,0)两点坐标 代入 ,即可求出b、c的值。
,即可求出b、c的值。
(2)利用轴对称和锐角三角函数求出点C的坐标,代入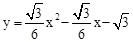 验证即可。
验证即可。
(3)通过证明△PAE∽△ECQ,求出时间t。
解:(1)∵二次函数 的图象与x轴交于点A(-2,0),B(3,0)两点,
的图象与x轴交于点A(-2,0),B(3,0)两点,
∴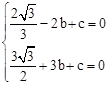 ,解得
,解得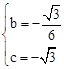 。
。
∴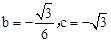 。
。
(2)证明:由(1)得二次函数解析式为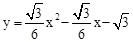 。
。
在正比例函数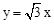 的图象上取一点F
的图象上取一点F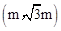 ,作FH⊥x轴于点H,则
,作FH⊥x轴于点H,则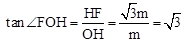 。∴
。∴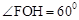 。
。
连接AC交 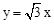 的图象于点E,作CK 垂直x轴于点K,
的图象于点E,作CK 垂直x轴于点K,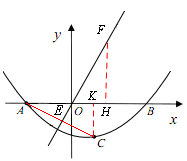
∵点A关于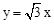 的图象的对称点为C,
的图象的对称点为C,
∴OE垂直平分AC。
∵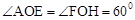 ,OA=2,
,OA=2,
∴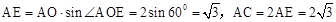 。
。
在Rt△ACK中,∵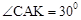 ,
,
∴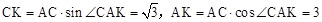 。∴
。∴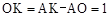 。
。
∴点C 的坐标为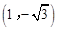 。
。
将C 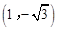 代入
代入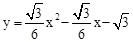 ,左边=右边,
,左边=右边,
∴点C在所求的二次函数的图象上。
(3)∵DB⊥x轴交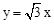 的图象于点D,B(3,0),
的图象于点D,B(3,0),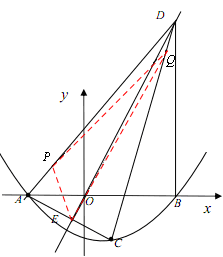
∴把x=3代入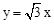 得
得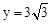 ,即BD=
,即BD=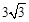 。
。
在Rt△ACK中,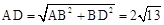 ,
,
∵OE垂直平分AC,
∴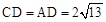 ,
,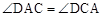 。
。
假设存在某一时刻,使PE平分∠APQ,同时QE平分∠PQC,
则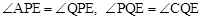 。
。
∵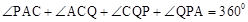 , ∴
, ∴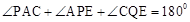 。
。
又∵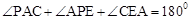 ,∴
,∴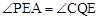 。
。
又∵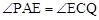 ,∴△PAE∽△ECQ。∴
,∴△PAE∽△ECQ。∴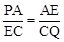 ,即
,即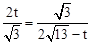 。
。
整理,得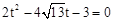 ,解得
,解得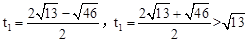 (不合题意,舍去)。
(不合题意,舍去)。
∴存在时刻 ,使PE平分∠APQ,同时QE平分∠PQC。
,使PE平分∠APQ,同时QE平分∠PQC。

 名校课堂系列答案
名校课堂系列答案如图,△ABO的面积为3,且AO=AB,双曲线y= 经过点A,则k的值为( )
经过点A,则k的值为( )
A. | B.3 | C.6 | D.9 |
已知反比例函数y= 的图象上有两点A(x1,y1)、B(x2,y2),当x1<0<x2时,有y1<y2,则m的取值范围是
的图象上有两点A(x1,y1)、B(x2,y2),当x1<0<x2时,有y1<y2,则m的取值范围是
A.m< | B.m>0 | C.m<0 | D.m> |

 与x轴交于点A,与y轴交于点B,将△AOB绕点O顺时针旋转90°后得到△COD.
与x轴交于点A,与y轴交于点B,将△AOB绕点O顺时针旋转90°后得到△COD.

 与x轴交于A.B两点,与y轴交于C点,抛物线的顶点为D点,点A的坐标为(﹣1,0).
与x轴交于A.B两点,与y轴交于C点,抛物线的顶点为D点,点A的坐标为(﹣1,0).

 与x轴交于点A和点B,与y轴交于点C,已知点B的坐标为(3,0).
与x轴交于点A和点B,与y轴交于点C,已知点B的坐标为(3,0).
 (a、m为常数,且a¹0)。
(a、m为常数,且a¹0)。