题目内容
【题目】如图,在等边△ABC中,点E为边AB上任意一点,点D在边CB的延长线上,且ED=EC.

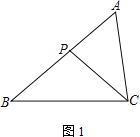
(1)当点E为AB的中点时(如图1),则有AE DB(填“>”“<”或“=”);
(2)猜想AE与DB的数量关系,并证明你的猜想.
【答案】(1)=; (2)见解析
【解析】试题分析:
(1)△BCE中可证,∠BCE=30°,又EB=EC,则∠D=∠ECB=30°,所以△BCE是等腰三角形,结合AE=BE即可;
(2)过E作EF∥BC交AC于F,用AAS证明△DEB≌△ECF.
试题解析:
(1)∵△ABC是等边三角形,∴∠ABC=60°,AB=AC=BC.
∵E为AB的中点,所以∠BCE=30°.
∵ED=EC,∴∠D=∠BCE=30°,∴∠BED=30°,∴∠D=∠BED,∴BD=BE,
∴BD=AE.
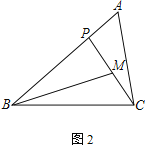
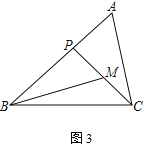
(2)当点E为AB上任意一点时,AE与DB的大小关系不会改变.理由如下:
过E作EF∥BC交AC于F,
∵△ABC是等边三角形,
∴∠ABC=∠ACB=∠A=60°,AB=AC=BC.
∴∠AEF=∠ABC=60°,∠AFE=∠ACB=60°,即∠AEF=∠AFE=∠A=60°.
∴△AEF是等边三角形.∴AE=EF=AF.
∵∠ABC=∠ACB=∠AFE=60°,
∴∠DBE=∠EFC=120°,∠D+∠BED=∠FCE+∠ECD=60°.
∵DE=EC,∴∠D=∠ECD.∴∠BED=∠ECF.
在△DEB和△ECF中,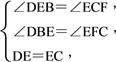
∴△DEB≌△ECF(AAS).
∴BD=EF=AE,即AE=BD.

【题目】盒子里装有红球和白球共10个,它们除颜色外其他都相同,每次从盒子里摸出1个球,记下颜色后放回盒子里摇匀再摸.在摸球活动中得到下列表中部分数据.
摸球次数 | 出现红球的频数 | 出现红球的频率 | 摸球次数 | 出现红球的频数 | 出现红球的频率 |
50 | 17 | 34% | 350 | 103 | 29.4% |
100 | 32 | 32% | 400 | 123 | |
150 | 44 | 29.3% | 450 | 136 | 30.2% |
200 | 64 | 32% | 500 | 148 | 29.6% |
250 | 78 | 31.2% | 550 | 167 | |
300 | 32% | 600 | 181 | 30.2% |
(1)请将表中数据补充完整.
(2)画出出现红球的频率的折线统计图.
(3)观察所画折线统计图,你发现了什么?
(4)你认为盒子里哪种颜色的球多?
(5)如果从盒子里任意摸出一球,你认为摸到白球的概率有多大?
【题目】某中学为了筹备校庆活动,准备印制一批校庆纪念册。该纪念册分A、B两种,每册都需要10张8K大小的纸,其中A纪念册有4张彩色页和6张黑白页组成;B纪念册有6张彩色页和4张黑白页组成。印制这批纪念册的总费用由制版费和印制费两部分组成,制版费与印数无关,价格为:彩色页300元∕张,黑白页50元∕张;印制费与总印数的关系见下表。
总印数 |
|
|
彩色(单位:元∕张) | 2.2 | 2.0 |
黑白(单位:元∕张) | 0.7 | 0.5 |
【1】印制这批纪念册的制版费为 元。
【2】若印制A、B两种纪念册各2千册,则共需多少费用?
【3】如果该校共印制了A、B两种纪念册6千册,一共花费了75500元,则该校印制了A、B两种纪念册各多少册?