题目内容
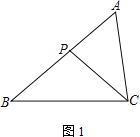
【题目】在△ABC中,P为边AB上一点.
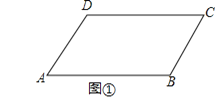
(1) 如图1,若∠ACP=∠B,求证:AC2=AP·AB;
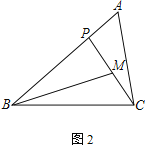
(2) 若M为CP的中点,AC=2,
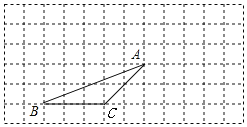
① 如图2,若∠PBM=∠ACP,AB=3,求BP的长;
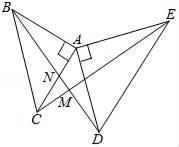
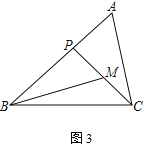
② 如图3,若∠ABC=45°,∠A=∠BMP=60°,直接写出BP的长.
【答案】(1)证明见解析;(2)①![]() ;②
;②![]()
【解析】试题分析:(1)根据已知条件易证△ACP∽△ABC,由相似三角形的性质即可证得结论;(2)①如图,作CQ∥BM交AB延长线于Q,设BP=x,则PQ=2x,易证△APC∽△ACQ,所以AC2=AP·AQ,由此列方程,解方程即可求得BP的长;②如图:作CQ⊥AB于点Q,作CP0=CP交AB于点P0,再证△AP0C∽△MPB,(2)的方法求得AP0的长,即可得BP的长.
试题解析:(1)证明:∵∠ACP=∠B,∠BAC=∠CAP,
∴△ACP∽△ABC,
∴AC:AB=AP:AC,
∴AC2=AP·AB;
(2)①如图,作CQ∥BM交AB延长线于Q,设BP=x,则PQ=2x
∵∠PBM=∠ACP,∠PAC=∠CAQ,
∴△APC∽△ACQ,
由AC2=AP·AQ得:22=(3-x)(3+x),∴x=![]()

即BP=![]() ;
;
②如图:作CQ⊥AB于点Q,作CP0=CP交AB于点P0,
∵AC=2,∴AQ=1,CQ=BQ=![]() ,
,
设AP0=x,P0Q=PQ=1-x,BP=![]() -1+x,
-1+x,
∵∠BPM=∠CP0A,∠BMP=∠CAP0,
∴△AP0C∽△MPB,∴![]() ,
,
∴MPP0C= AP0BP=x(
AP0BP=x(![]() -1+x),
-1+x),
解得x=![]()
∴BP=![]() -1+
-1+![]() =
=![]() .
.


练习册系列答案
相关题目