题目内容
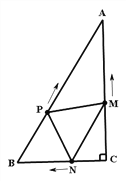
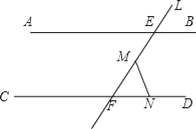
【题目】如图:AB∥CD,直线l交AB、CD分别于点E、F,点M在EF上,N是直线CD上的一个动点(点N不与F重合)
(1)当点N在射线FC上运动时,∠FMN+∠FNM=∠AEF,说明理由;
(2)当点N在射线FD上运动时,∠FMN+∠FNM与∠AEF有什么关系并说明理由.

【答案】(1)证明见解析;(2)∠FMN+∠FNM+∠AEF=180°,理由见解析.
【解析】试题分析:(1)利用两直线平行,同旁内角互补和三角形的内角和为180°,易得∠FMN+∠FNM=∠AEF;
(2)根据两直线平行,内错角相等和三角形的内角和为180°,易得∠FMN+∠FNM+∠AEF=180°.
解:(1)∵AB∥CD,
∴∠AEF+∠MFN=180°.
∵∠MFN+∠FMN+∠FNM=180°,
∴∠FMN+∠FNM=∠AEF.
(2)∠FMN+∠FNM+∠AEF=180°.
理由:∵AB∥CD,
∴∠AEF=∠MFN.
∵∠MFN+∠FMN+∠FNM=180°,
∴∠FMN+∠FNM+∠AEF=180°.

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案
相关题目