题目内容
【题目】如图,在平面直角坐标系中,抛物线![]() 的解析式为
的解析式为![]() ,将抛物线
,将抛物线![]() 沿
沿![]() 轴翻折得到抛物线
轴翻折得到抛物线![]() ,抛物线
,抛物线![]() 、
、![]() 的顶点分别为
的顶点分别为![]() 、
、![]() ,点
,点![]() 为抛物线
为抛物线![]() 上一点,横坐标为
上一点,横坐标为![]() ,过点
,过点![]() 作
作![]() 轴的平行线交抛物线
轴的平行线交抛物线![]() 于点
于点![]() .
.
(1)当![]() 时;
时;
①请直接写出抛物线![]() 的解析式;
的解析式;
②当![]() 时,求
时,求![]() 的值;
的值;
(2)当![]() 时.
时.
①![]() 为抛物线
为抛物线![]() 上一动点,当
上一动点,当![]() 为等腰直角三角形时,求
为等腰直角三角形时,求![]() 的值;
的值;
②以![]() 为边向左作正方形
为边向左作正方形![]() ,设横坐标为整数的点称为“梦想点”,当正方形
,设横坐标为整数的点称为“梦想点”,当正方形![]() 的内部(不包括边上)有6个“梦想点”时,直接写出
的内部(不包括边上)有6个“梦想点”时,直接写出![]() 的取值范围.
的取值范围.
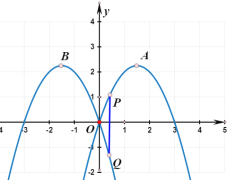
【答案】(1)①![]() ;②
;②![]() ,2;(2)①
,2;(2)①![]() ,
,![]() ,
,![]() ;②
;②![]() <m≤
<m≤![]()
【解析】
(1)①将抛物线对折,即将原来抛物线的x变为-x,代入可得;
②只需点A到直线PQ的距离的3倍与点B到直线PQ的距离相等即可;
(2)①存在3种情况,一种是PM=MQ,第二种是PM=PQ,第三种是PQ=QM,分别按照等腰直角三角形的性质可求得;
②正方形的边长为8m,根据“梦想点”的定义,可得边长取值范围为:2<8m≤3.
(1)①∵抛物线![]() 的解析式为
的解析式为![]() ,将抛物线
,将抛物线![]() 沿
沿![]() 轴翻折得到抛物线
轴翻折得到抛物线![]()
∴将![]() 中的x变为-x代入,求得的即为
中的x变为-x代入,求得的即为![]() 的解析式
的解析式
即:![]()
化简得;![]() ,将m=1代入得:
,将m=1代入得:![]()
②∵m=1
∴![]() :
:![]() ,
,![]() :
:![]()
∴A(1,1),B(-1,1),P的横坐标为n
∴AP的距离=![]() ,BP的距离=n-1
,BP的距离=n-1
∵![]()
∴n-1=3![]()
解得:n=![]() 或n=2
或n=2
(2)①情况一:PM=MQ,图形如下,过点M作PQ的垂线,交PQ于点N
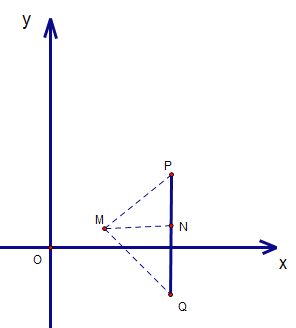
由题意得:P(2,-4+4m),Q(2,-4-4m)
∴PQ=![]()
∵△MPQ是等腰直角三角形,MP=MQ
∴∠MPN=45°,∴△MPN是等腰直角三角形,MN=NP
设点M(x,![]() )
)
∵MN是PQ的垂直平分线,∴点N、M的纵坐标为:![]() ,点N的横坐标为:2
,点N的横坐标为:2
∴-4=![]()
∵MN=NP,∴2-x=![]() ,化简得:x=2-4m,代入上式并化简得:
,化简得:x=2-4m,代入上式并化简得:
8![]()
解得:m=0(舍),或m=![]()
情况二:PM=PQ,图形如下
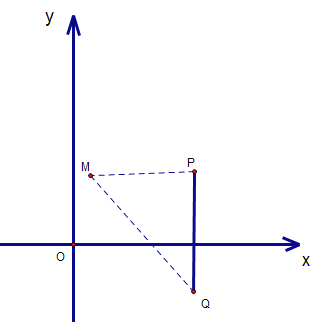
∵PM=PQ,∴2-x=8m,化简得:x=2-8m
∵△MPQ是等腰直角三角形,∠MPQ=90°
∴点M的纵坐标与点P的纵坐标相等,即![]()
将x=2-8m代入上式并化简得:![]()
解得:m=0(舍),或m=![]()
情况三:QM=PQ,图形如下
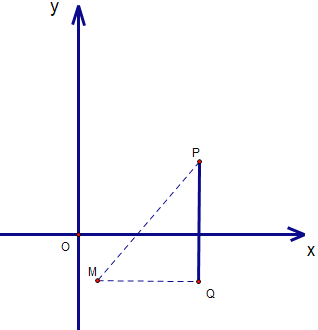
∵MQ=PQ,∴2-x=8m,化简得:x=2-8m
∵△MPQ是等腰直角三角形,∠MQP=90°
∴点M的纵坐标与点Q的纵坐标相等,即![]()
将x=2-8m代入上式并化简得:![]()
解得:m=0(舍),或m=![]()
②∵PQ=8m,四边形PQDE是正方形,∴正方形的边长为8m
根据梦想点定义,见下面2个图形
如图1:
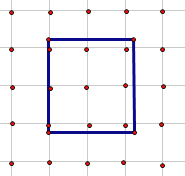
当正方形的边长刚好比2大一点点的时候,正方形内包含的梦想点为6个
∴8m>2,解得:m>![]()
如图2:
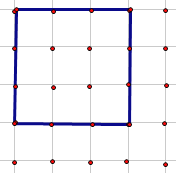
当正方形的边长为3时,刚好有4个梦想点,边长在增加一点,则会有9个梦想点
∴8m≤3,解得:m≤![]()
∴![]() <m≤
<m≤![]()

 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案【题目】某中学初三年级积极推进走班制教学.为了了解一段时间以来,“至善班”的学习效 果,年级组织了多次定时测试,现随机选取甲、乙两个“至善班”,从中各抽取![]() 名同学在某一次定时测试中的数学成绩,其结果记录如下:
名同学在某一次定时测试中的数学成绩,其结果记录如下:
收集数据:
“至善班”甲班![]() 的名同学的数学成绩统计(满分为 100 分)(单位:分)
的名同学的数学成绩统计(满分为 100 分)(单位:分)
![]()
![]()
“至善班”乙班的![]() 名同学的数学成绩统计(满分为 100 分)(单位:分)
名同学的数学成绩统计(满分为 100 分)(单位:分)
![]()
![]()
整理数据:(成绩得分用![]() 表示)
表示)
分数 数量 班级 |
|
|
|
|
|
甲班(人数) | 1 | 3 | 4 | 6 | 6 |
乙班(人数) | 1 | 1 | 8 | 6 | 4 |
分析数据,并回答下列问题:
![]() 完成下表:
完成下表:
平均数 | 中位数 | 众数 | |
甲班 |
|
|
|
乙班 |
|
|
|
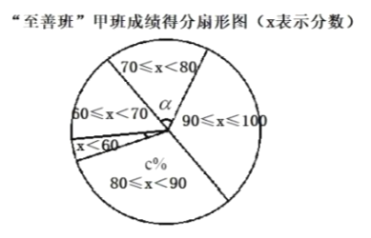
![]() 在“至善班”甲班的扇形图中, 成绩在
在“至善班”甲班的扇形图中, 成绩在![]() 的扇形中,所对的圆心角
的扇形中,所对的圆心角![]() 的度数为 . 估计全部“至善班”的
的度数为 . 估计全部“至善班”的![]() 人中优秀人数为 人.(
人中优秀人数为 人.(![]() 分及以上为优秀).
分及以上为优秀).
![]() 根据以上数据,你认为“至善班” 班(填“甲”或“乙”)所选取做样本 的同学的学习效果更好一些,你所做判断的理由是:
根据以上数据,你认为“至善班” 班(填“甲”或“乙”)所选取做样本 的同学的学习效果更好一些,你所做判断的理由是:
①
②
【题目】调查作业:了解你所住小区家庭3月份用气量情况.
小天、小东和小芸三位同学住在同一小区,该小区共有300户家庭,每户家庭人数在2—5之间,这300户家庭的平均人数约为3.3.
小天、小东和小芸各自对该小区家庭3月份用气量情况进行了抽样调查,将收集的数据进行了整理,绘制的统计表分别为表1、表2、表3,
表1抽样调查小区4户家庭3月份用气量统计表(单位:![]() )
)
家庭人数 | 2 | 3 | 4 | 5 |
用气量 | 14 | 19 | 21 | 26 |
表2抽样调查小区15户家庭3月份用气量统计表(单位:![]() )
)
家庭人数 | 2 | 2 | 2 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 4 |
用气量 | 10 | 11 | 15 | 13 | 14 | 15 | 17 | 17 | 18 | 18 | 18 | 18 | 18 | 20 | 22 |
表3抽样调查小区15户家庭3月份用气量统计表(单位:![]() )
)
家庭人数 | 2 | 2 | 2 | 3 | 3 | 3 | 3 | 3 | 3 | 4 | 4 | 4 | 4 | 5 | 5 |
用气量 | 10 | 12 | 13 | 14 | 17 | 17 | 18 | 20 | 20 | 21 | 22 | 26 | 31 | 28 | 31 |
根据以上材料回答问题:
(1)小天、小东和小芸三人中,哪一位同学抽样调查的数据能较好地反应出该小区家庭3月份用气量情况?请简要说明其他两位同学抽样调查的不足之处;
(2)小东将表2中的数据按用气量![]() 大小分为三类;
大小分为三类;
①节约型:![]() ;
;
②居中型:![]() ;
;
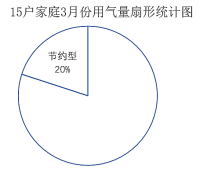
③偏高型:![]() ;并绘制成如下扇形统计图,请帮助他将扇形图补充完整;
;并绘制成如下扇形统计图,请帮助他将扇形图补充完整;
(3)小芸算出表3中3月份平均每人的用量为![]() ,请估计该小区3月份的总用气量.
,请估计该小区3月份的总用气量.
【题目】已知函数![]() ,小李同学对该函数的图象与性质进行了探究,下面是小李同学探究的过程,补充完整:
,小李同学对该函数的图象与性质进行了探究,下面是小李同学探究的过程,补充完整:
(1)直接写出自变量x的取值范围:__________;
(2)下表是y与x的几组对应值:
x | … | -4 | -1 | 0 |
| 1 |
|
| 3 |
| 4 | 5 | n | … |
y | … |
| m |
| 0 | -1 | -4 | 8 | 5 | 4 |
| 3 |
| … |
则m= ,n= ;
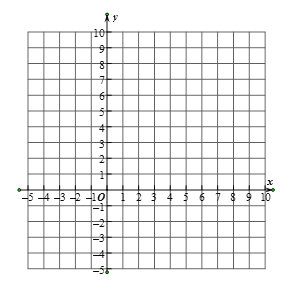
(3)如图所示,在平面直角坐标系xoy中,描出以上表中各对对应值为坐标的点,并根据描出的点,画出该函数的图象;
(4)观察函数图象可知:该函数图象的对称中心的坐标是______;
(5)当![]() 时,关于x的方程
时,关于x的方程![]() 有实数解,直接写出k的取值范围_______.
有实数解,直接写出k的取值范围_______.