题目内容
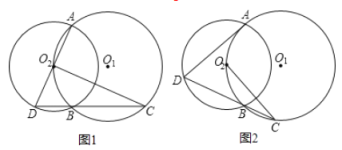
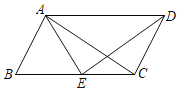
【题目】如图,在平行四边形ABCD中,AB=AE.若AE平分∠DAB,∠EAC=25°,则∠B=_____,∠AED的度数为_____.
【答案】60° 85°
【解析】
先证△ABC≌△EAD(SAS),得出∠BAC=∠AED,再证△ABE为等边三角形.得出∠B=∠BAE=60°,求出∠BAC=85°,即可得出答案.
解:∵四边形ABCD为平行四边形,
∴AD∥BC,AD=BC.
∴∠DAE=∠AEB.
∵AB=AE,
∴∠AEB=∠B.
∴∠B=∠DAE.
∵在△ABC和△EAD中, ,
,
∴△ABC≌△EAD(SAS),
∴∠BAC=∠AED,
∵AE平分∠DAB,
∴∠DAE=∠BAE;
又∵∠DAE=∠AEB,
∴∠BAE=∠AEB=∠B.
∴△ABE为等边三角形.
∴∠B=∠BAE=60°,
∵∠EAC=25°,
∴∠BAC=85°,
∴∠AED=85°.
故答案为:60°,85°.

练习册系列答案
相关题目