题目内容
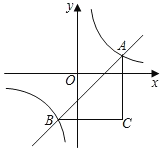
【题目】如图，直线y＝x+m与双曲线y＝
交于A，B两点，作BC∥x轴，AC∥y轴，交BC于点C，则S△ABC的最小值是_____．
【答案】12
【解析】
设A(a，
)，B(b，
)，则C(a，)．将y＝x+m代入y＝
得x+m＝，得到a+b＝﹣m，ab＝﹣6，求得S△ABC＝
m2+12，进而即可求得△ABC的面积的最小值．
设A(a，)，B(b，)，则C(a，)．
将y＝x+m代入y＝，得x+m＝，整理，得x2+mx﹣6＝0，
∴a+b＝﹣m，ab＝﹣6，
∴（a﹣b）2＝（a+b）2﹣4ab＝m2+24．
∵S△ABC＝ACBC
＝（﹣）（a﹣b）
＝
（a﹣b）
＝（a﹣b）2
＝（m2+24）
＝m2+12，
∴当m＝0时，△ABC的面积有最小值12．
故答案为12．
练习册系列答案
初中学业考试导与练系列答案
相关题目
