Question

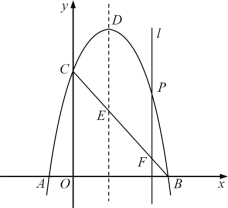
【题目】在平面直角坐标系xOy中，二次函数y=ax2﹣2ax+c的图象经过点A（﹣1，1），将A点向右平移3个单位长度，再向上平移2个单位长度，得到点B，直线y=2x+m经过点B，与y轴交于点C．

（1）求点B，C的坐标；

（2）求二次函数图象的对称轴；

（3）若二次函数y=ax2﹣2ax+c（﹣1＜x＜2）的图象与射线CB恰有一个公共点，结合函数图象，直接写出a的取值范围．

Answer 1

【答案】（1）B（2，3），C（0，﹣1）；（2）；（3）或

【解析】

（1）由平移的性质可求点B坐标，代入解析式可求m的值，从而可求得直线解析式，即可求点C坐标；

（2）根据二次函数的对称轴为x=﹣，即可求解；

（3）结合图形，分类讨论，分a＞0时和a＜0时，即可求解．

解：（1）∵点A（﹣1，1）向右平移3个单位长度，再向上平移2个单位长度，得到点B，

∴点B（2，3），

∵直线y=2x+m经过点B，

∴3=4+m，

∴m=﹣1，

∴直线解析式为：y=2x﹣1，

∵直线y=2x+m与y轴交于点C，

∴点C（0，﹣1）；

（2）二次函数y=ax2﹣2ax+c的对称轴为直线x=﹣=1；

（3）∵二次函数y=ax2﹣2ax+c的图象经过点A（﹣1，1），

∴1=a+2a+c，

∴c=1﹣3a，

∴抛物线解析式为：y=ax2﹣2ax+1﹣3a，

∴顶点坐标为（1，1﹣4a），

当a＞0时，如图所示，

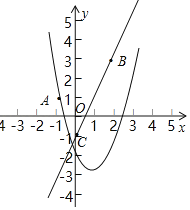
∴当1﹣4a＜1时，二次函数y=ax2﹣2ax+c（﹣1＜x＜2）的图象与射线CB恰有一个公共点，

∴a＞0；

当a＜0时，如图所示，

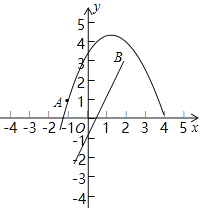
∴4a﹣4a+1﹣3a＞3，

∴a＜﹣，

综上所述：当a＞0或a＜﹣时，二次函数y=ax2﹣2ax+c（﹣1＜x＜2）的图象与射线CB恰有一个公共点．