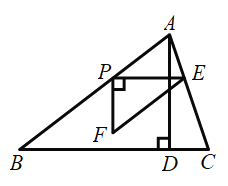
题目内容
【题目】如图,在![]() 中,
中,![]() 于点
于点![]() ,动点
,动点![]() 从点
从点![]() 出发以每秒
出发以每秒![]() 个单位长度的速度向终点
个单位长度的速度向终点![]() 运动,当点
运动,当点![]() 与点
与点![]() 不重合时,过点
不重合时,过点![]() 作
作![]() 交边
交边![]() 于点
于点![]() ,以
,以![]() 为边作
为边作![]() 使
使![]() 点
点![]() 在点
在点![]() 的下方,且
的下方,且![]() ,设
,设![]() 与
与![]() 重叠部分图形的面积为
重叠部分图形的面积为![]() ,点
,点![]() 的运动时间为
的运动时间为![]() 秒.
秒.
(1)![]() 的长为 ;
的长为 ;
(2)当点![]() 落在边
落在边![]() 上时,求
上时,求![]() 的值;
的值;
(3)当![]() 与
与![]() 重叠部分图形为四边形时,求
重叠部分图形为四边形时,求![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(4)若射线![]() 与边
与边![]() 交于点
交于点![]() 连结
连结![]() ,当
,当![]() 的垂直平分线经过
的垂直平分线经过![]() 的顶点时,直接写出
的顶点时,直接写出![]() 的值.
的值.
【答案】(1)2;(2)![]() ;(3)当0<t≤
;(3)当0<t≤![]() 时,
时,![]() ;
;![]() ≤t<2时,
≤t<2时,![]() ;(4)
;(4)![]() 或
或![]() 或
或![]() .
.
【解析】
(1)由勾股定理计算出BD即可得到CD的长度;
(2)当点F落在BC上时,四边形BFEP为平行四边形,利用锐角三角函数的定义表达出BF,根据PE=BF列出方程解答即可;
(3)分别求出当EF经过点D时,以及当点F在边BC上时的时间t,再分类讨论,当0<t≤![]() 时,重叠部分为四边形PNDM;
时,重叠部分为四边形PNDM;![]() ≤t<2时,△PEF与△ABD重叠的部分为四边形PFHG,分别根据锐角三角函数的定义以及相似三角形的相似比,表达出面积即可;
≤t<2时,△PEF与△ABD重叠的部分为四边形PFHG,分别根据锐角三角函数的定义以及相似三角形的相似比,表达出面积即可;
(4)分三种情况讨论,①当PQ的中垂线过点B时,证明平行四边形PBQE是菱形,再根据PE=BP列出等式求解即可;②当PQ的中垂线过点A时,在Rt△AQD中,根据AD2+QD2=AQ2即可解答;③当PQ的中垂线经过点C时,根据CQ=PC列出等式即可解答.
(1)由题意可知,BD=![]() ,
,
∴CD=BC-BD=10-8=2,
故答案为:2;
(2)如图,当点F落在BC上时,由题意可知,BP=5t,则AP=10-5t,
∵PE∥BC,EF∥AB,
则四边形BFEP为平行四边形,且∠AEP=∠ACB,
又∵∠ACB=∠BAC,
∴∠AEP=∠BAC,
∴PE=AP=10-5t,
又∵cosB=![]() ,
,
∴![]() ,则BF=4t,
,则BF=4t,
∵四边形BFEP为平行四边形,
∴PE=BF,即![]() ,解得:
,解得:![]() ,
,
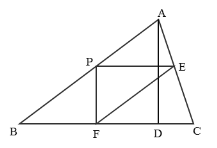
(3)①如下图所示,当EF经过点D时,
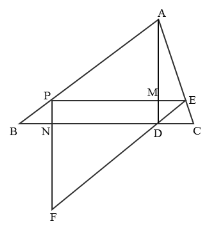
∵PE∥BC,EF∥AB,
∴四边形PBDE是平行四边形,且∠DEC=∠BAC,
∴DE=BP=5t,∠DEC=∠C,
∴DE=DC,即5t=2,解得t=![]() ,
,
∴当0<t≤![]() 时,重叠部分为四边形PNDM,
时,重叠部分为四边形PNDM,
∵∠EPF=90°,PE∥BC,
∴∠PND=90°,
又∵∠ADB=90°,
∴四边形PNDM为矩形,
在RT△BPN中,sinB=![]() ,即
,即![]() ,解得PN=3t,
,解得PN=3t,
cosB=![]() ,即
,即![]() ,解得BN=4t,
,解得BN=4t,
∴DN=8-4t,
∴S=PN·DN=![]() ,
,
②当点F在边BC上时,如图,
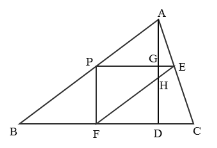
由①可知BF=4t,PF=3t,则CF=10-4t,
由EF=CF可得:5t=10-4t,解得:![]() ,
,
∴![]() ≤t<2时,△PEF与△ABD重叠的部分为四边形PFHG,
≤t<2时,△PEF与△ABD重叠的部分为四边形PFHG,
∵PE∥BC,
∴△APG∽△ABD,
∴![]() ,即
,即![]() ,解得:PG=
,解得:PG=![]() ,
,
∵PE=AP=10-5t,
∴GE=10-5t-![]() =
=![]() ,
,
∵EF∥AB,
∴∠EHG=∠BAD,
∴tan∠EHG=tan∠BAD,即![]() ,
,
∴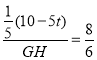 ,解得:GH=
,解得:GH=![]() ,
,
又∵∠PFE=∠EHG,则∠PFE=∠BAD
∴tan∠PFE=tan=∠BAD,即![]() ,解得:PF=
,解得:PF=![]() ,
,
∴![]() ,
,
综上所述:当0<t≤![]() 时,
时,![]() ;
;![]() ≤t<2时,
≤t<2时,![]() ;
;
(4)①当PQ的中垂线过点B时,如图,即BE是PQ的中垂线,
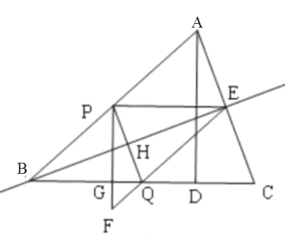
∵四边形PBQE是平行四边形,BE垂直PQ,
∴平行四边形PBQE是菱形,
∴PE=BP,即5t=10-5t,解得:t=1,
②当PQ的中垂线过点A时,如图,连接AE,则AP=AQ=10-5t,
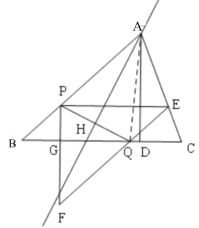
∵CQ=EQ=5t,
∴QD=CQ-CD=5t-2,
∴在Rt△AQD中,AD2+QD2=AQ2,即![]() ,解得:
,解得:![]() ,
,
③当PQ的中垂线经过点C时,如图,连接PC,延长PF交BC于点K,
则CQ=PC,
∵∠EPF=90°,PE∥BC,
∴∠PKC=90°,
∵BK=4t,PK=3t,则CK=10-4t,
∴PC=![]() ,
,
又∵CQ=QE=BP=5t,
∴5t=![]() ,解得:
,解得:![]() ,
,
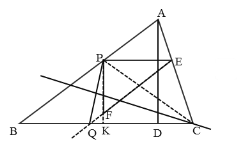
综上所述:![]() 或
或![]() 或
或![]() .
.

【题目】深圳天虹某商场从厂家批发电视机进行零售,批发价格与零售价格如下表:
电视机型号 | 甲 | 乙 |
批发价(元/台) | 1500 | 2500 |
零售价(元/台) | 2025 | 3640 |
若商场购进甲、乙两种型号的电视机共50台,用去9万元.
(1)求商场购进甲、乙型号的电视机各多少台?
(2)迎“元旦”商场决定进行优惠促销:以零售价的七五折销售乙种型号电视机,两种电视机销售完毕,商场共获利8.5%,求甲种型号电视机打几折销售?