题目内容
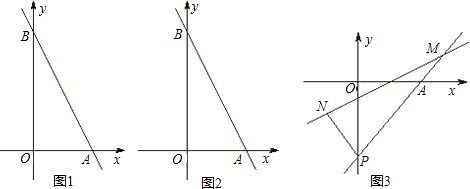
若一次函数y=-
x+b（b＞0）与x，y轴分别交于A，B两点，
（1）直接写出A、B两点的坐标（用含b的代数式表示）
（2）当b=2时，求△OAB的周长．
| 3 |
| 4 |
（1）直接写出A、B两点的坐标（用含b的代数式表示）
（2）当b=2时，求△OAB的周长．
（1）∵令y=0，则-
x+b=0，解得x=
b；令x=0，则y=b，
∴直线y=-
x+b与x轴的交点坐标A（
b，0），与y轴交点坐标B（0，b）；
（2）∵b=2，
∴OA=
，OB=2，OC=
=
=
∴△OAB的周长=OA+OB+OC=8．
| 3 |
| 4 |
| 4 |
| 3 |
∴直线y=-
| 3 |
| 4 |
| 4 |
| 3 |
（2）∵b=2，
∴OA=
| 8 |
| 3 |
| OA2+OB2 |
(
|
| 10 |
| 3 |
∴△OAB的周长=OA+OB+OC=8．
练习册系列答案
相关题目
