��Ŀ����
��ͼ1����ƽ��ֱ������ϵ�У�A��a��0����B��0��b������a��b����b=
��
��1����ֱ��AB�Ľ���ʽ��
��2������MΪֱ��y=mx�ڵ�һ������һ�㣬�ҡ�ABM�ǵ���ֱ�������Σ���m��ֵ��
��3����ͼ3����A��ֱ��y=kx-2k��y�Ḻ�����ڵ�P��N��ĺ�����Ϊ-1����N���ֱ��y=
x-
��AP�ڵ�M�������������ۣ���
��ֵ�Dz��䣻��
��ֵ�Dz��䣬ֻ��һ����������ȷ�������жϳ���ȷ�Ľ��ۣ�������֤���������ֵ��
| ||||
| a+2 |
��1����ֱ��AB�Ľ���ʽ��
��2������MΪֱ��y=mx�ڵ�һ������һ�㣬�ҡ�ABM�ǵ���ֱ�������Σ���m��ֵ��
��3����ͼ3����A��ֱ��y=kx-2k��y�Ḻ�����ڵ�P��N��ĺ�����Ϊ-1����N���ֱ��y=
| k |
| 2 |
| k |
| 2 |
| PM+PN |
| NM |
| PM-PN |
| AM |

��1��Ҫʹb=
�����壬
����a2-4��0��4-a2��0��a+2��0��
��a=2��
����ã�b=4��
��A��2��0����B��0��4����
��ֱ��AB�Ľ���ʽ��y=kx+b��
����ã�
��
��ã�k=-2��b=4��
�ຯ������ʽΪ��y=-2x+4��
��ֱ��AB�Ľ���ʽ��y=-2x+4��
��2����ͼ2�������������
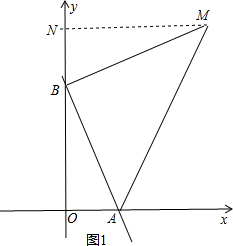
����ͼ1����BM��BA����BM=BAʱ����M��MN��y����N��
��BM��BA��MN��y�ᣬOB��OA��
���MBA=��MNB=��BOA=90�㣬
���NBM+��NMB=90�㣬��ABO+��NBM=90�㣬
���ABO=��NMB��
�ڡ�BMN�͡�ABO��
��
���BMN�ա�ABO��AAS����
MN=OB=4��BN=OA=2��
��ON=2+4=6��
��M��������4��6����
����y=mx�ã�m=
��
����ͼ2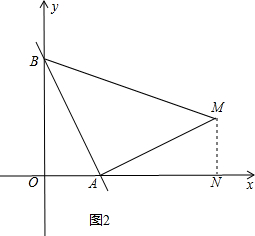
��AM��BA����AM=BAʱ����M��MN��x����N����BOA�ա�ANM��AAS����ͬ�����M������Ϊ��6��2����m=
��
����ͼ4��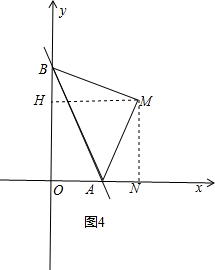
��AM��BM����AM=BMʱ����M��MN��X����N��MH��Y����H�����BHM�ա�AMN��
��MN=MH��
��M��x��x������y=mx�ã�x=mx��
��m=1��
��m��ֵ��
��
��1��
��3����ͼ3������2����ȷ���Ҷ�ֵΪ2��
��NM��x��Ľ���ΪH����M��MG��x����G����H��HD��x�ᣬHD��MP��D�㣬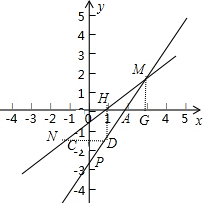 ����ND��
����ND��
��y=
x-
��x�ύ��H�㣬
��H��1��0����
��y=
x-
��y=kx-2k����M�㣬
��M��3��k����
��A��2��0����
��AΪHG���е㣬
���AMG�ա�ADH��ASA����
����ΪN��ĺ�����Ϊ-1������y=
x-
�ϣ�
��ɵ�N��������Ϊ-k��ͬ��P��������Ϊ-2k��
��NDƽ����x����N��D�ĺ�����ֱ�Ϊ-1��1
��N��D����y��Գƣ�
�ߡ�AMG�ա�ADH�ա�DPC�ա�NPC��
��PN=PD=AD=AM��
��
=2��
| ||||
| a+2 |
����a2-4��0��4-a2��0��a+2��0��
��a=2��
����ã�b=4��
��A��2��0����B��0��4����
��ֱ��AB�Ľ���ʽ��y=kx+b��
����ã�
|
��ã�k=-2��b=4��
�ຯ������ʽΪ��y=-2x+4��
��ֱ��AB�Ľ���ʽ��y=-2x+4��
��2����ͼ2�������������

����ͼ1����BM��BA����BM=BAʱ����M��MN��y����N��
��BM��BA��MN��y�ᣬOB��OA��
���MBA=��MNB=��BOA=90�㣬
���NBM+��NMB=90�㣬��ABO+��NBM=90�㣬
���ABO=��NMB��
�ڡ�BMN�͡�ABO��
|
���BMN�ա�ABO��AAS����
MN=OB=4��BN=OA=2��
��ON=2+4=6��
��M��������4��6����
����y=mx�ã�m=
| 3 |
| 2 |
����ͼ2

��AM��BA����AM=BAʱ����M��MN��x����N����BOA�ա�ANM��AAS����ͬ�����M������Ϊ��6��2����m=
| 1 |
| 3 |
����ͼ4��

��AM��BM����AM=BMʱ����M��MN��X����N��MH��Y����H�����BHM�ա�AMN��
��MN=MH��
��M��x��x������y=mx�ã�x=mx��
��m=1��
��m��ֵ��
| 3 |
| 2 |
| 1 |
| 3 |
��3����ͼ3������2����ȷ���Ҷ�ֵΪ2��
��NM��x��Ľ���ΪH����M��MG��x����G����H��HD��x�ᣬHD��MP��D�㣬
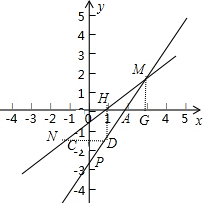 ����ND��
����ND����y=
| k |
| 2 |
| k |
| 2 |
��H��1��0����
��y=
| k |
| 2 |
| k |
| 2 |
��M��3��k����
��A��2��0����
��AΪHG���е㣬
���AMG�ա�ADH��ASA����
����ΪN��ĺ�����Ϊ-1������y=
| k |
| 2 |
| k |
| 2 |
��ɵ�N��������Ϊ-k��ͬ��P��������Ϊ-2k��
��NDƽ����x����N��D�ĺ�����ֱ�Ϊ-1��1
��N��D����y��Գƣ�
�ߡ�AMG�ա�ADH�ա�DPC�ա�NPC��
��PN=PD=AD=AM��
��
| PM-PN |
| AM |

��ϰ��ϵ�д�
 ��������ϵ�д�
��������ϵ�д�
�����Ŀ








 ��OA��OB��������P��O���������·��O?B?A��ÿ��1����λ���ȵ��ٶ��˶�������A��ʱ�˶�ֹͣ��
��OA��OB��������P��O���������·��O?B?A��ÿ��1����λ���ȵ��ٶ��˶�������A��ʱ�˶�ֹͣ��