Question

【题目】已知某种月饼形状的俯视图如图1所示，该形状由1个正六边形和6个半圆组成，半圆直径与正六边形的边长相等．

现商家设计了2种棱柱体包装盒，其底面分别为矩形和正六边形(如图2和图3)我们可从底面的利用率来记算整个包装盒的利用情况．(底面利用率=×100%)

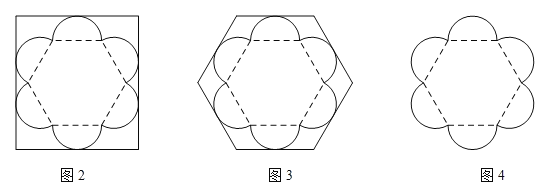
（1）请分别计算出图2与图3中的底面利用率(结果保留到0.1%)；

（2）考虑到节约成本，商家希望底面利用率能够不低于80%，且底面图形仍然采用最基本的几何形状，请问商家的要求是否能够满足，若可以满足，请设计一种方案，并直接写出此时的利用率；若不能满足，请说明理由．

Answer 1

【答案】（1）图2、3的底面利用率分别约为66.4%、40.2%；（2）设计底面为圆形的包装盒，利用率约为84.5%.

【解析】

（1）设半圆直径与正六边形的边长为a，根据正多边形和圆的知识，算出月饼面积，再算出图2正方形的边长，即可求出图2的面积，和图2底面的利用率；图3的包装盒六边形和月饼相似，利用面积比等于相似比的平方，求出图3包装盒的底面利用率；

（2）设计底面为圆形的包装盒，求出其半径、面积、底面利用率，满足底面利用率不低于80%.

解：（1）设半圆直径与正六边形的边长a，连接正六边形的中心和两相邻的顶点，则,,

∴是等边三角形，

∴=a,

过点作,

∴，,

∴=，

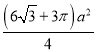延长OC与其中一个半圆交于点D，

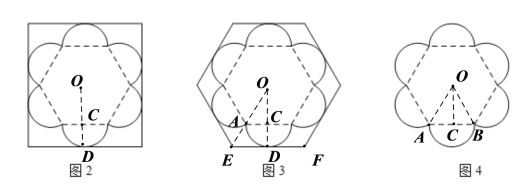
则，

∴,

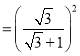
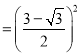
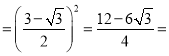
40.2%;

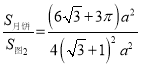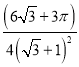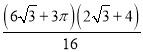===66.4%;

答：图2、3的底面利用率分别约为66.4%、40.2%；

（2）商家的要求是否能够满足，设计如图所示底面为圆的包装盒，半径为，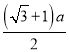

=，

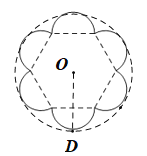
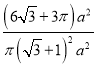答：设计底面为圆形的包装盒，利用率约为84.5%.