题目内容
【题目】在△ABC中,AB=AC
(1)求作一点P,使点P为△ABC的外接圆圆心.(保留作图痕迹,不写作法)
(2)若∠A=50°,求∠PBC的度数.
【答案】(1)见解析;(2)∠PBC的度数为40°
【解析】
(1)分别作BC和AC的垂直平分线,它们的交点P即为△ABC的外接圆圆心.
(2)根据题意可知AB=AC,∠BAC=50°,求出∠BAD的度数,进而根据PA=PB求出∠BPD的度数,后根据∠BDP=90°求得∠PBC=40°.
解:(1)如图,点P即为△ABC的外接圆圆心;
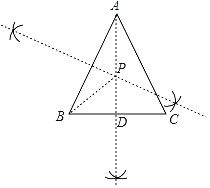
(2)∵AB=AC,∠BAC=50°,
∴AD⊥BC,∠BAD=![]() ∠BAC=25°,
∠BAC=25°,
∵PA=PB,
∴∠BPD=2∠BAP=50°,
∵∠BDP=90°,
∴∠PBD=90°﹣50°=40°.
即∠PBC=40°
答:∠PBC的度数为40°.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目