题目内容
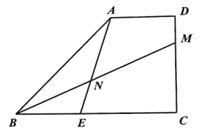
【题目】如图,在梯形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,点
,点![]() 在边
在边![]() 上,
上,![]() ,点
,点![]() 是射线
是射线![]() 上一个动点(不与点
上一个动点(不与点![]() 、
、![]() 重合),联结
重合),联结![]() 交射线
交射线![]() 于点
于点![]() ,设
,设![]() ,
,![]() .
.
(1)求![]() 的长;
的长;
(2)当动点![]() 在线段
在线段![]() 上时,试求
上时,试求![]() 与
与![]() 之间的函数解析式,并写出函数的定义域;
之间的函数解析式,并写出函数的定义域;
(3)当动点![]() 运动时,直线
运动时,直线![]() 与直线
与直线![]() 的夹角等于
的夹角等于![]() ,请直接写出这时线段
,请直接写出这时线段![]() 的长.
的长.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)线段
;(3)线段![]() 的长为
的长为![]() 或13
或13
【解析】
(1)如图1中,作AH⊥BC于H,解直角三角形求出EH,CH即可解决问题.
(2)延长AD交BM的延长线于G.利用平行线分线段成比例定理构建关系式即可解决问题.
(3)分两种情形:①如图3-1中,当点M在线段DC上时,∠BNE=∠ABC=45°.②如图3-2中,当点M在线段DC的延长线上时,∠ANB=∠ABE=45°,利用相似三角形的性质即可解决问题.
:(1)如图1中,作AH⊥BC于H,
∵AD∥BC,∠C=90°,

∴∠AHC=∠C=∠D=90°,
∴四边形AHCD是矩形,
∴AD=CH=2,AH=CD=3,
∵tan∠AEC=3,
∴![]() =3,
=3,
∴EH=1,CE=1+2=3,
∴BE=BC-CE=5-3=2.
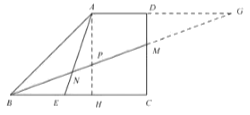
(2)延长![]() ,
,![]() 交于点
交于点![]() ,
,
∵AG∥BC,
∴![]() ,
,
∴![]() ,
,![]()
∵![]() ,
,
∴ .
.
解得:![]()
(3)①如图3-1中,当点M在线段DC上时,∠BNE=∠ABC=45°,
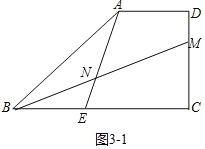
∵![]() ,
,
![]() ,
,
则有![]() ,解得:
,解得:![]()
②如图3-2中,当点M在线段DC的延长线上时,∠ANB=∠ABE=45°,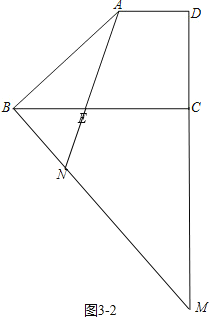
∵![]() ,
,
∴![]() ,
,
则有 ,
,
解得![]()
综上所述:线段![]() 的长为
的长为![]() 或13.
或13.

练习册系列答案
相关题目