Question

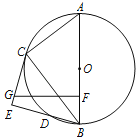
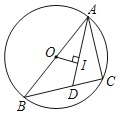
【题目】如图，⊙O是△ABC的外接圆，AB是⊙O的直径，I为△ABC的内心，AI的延长线交BC于D，若OI⊥AD，则sin∠CAD的值为（ ）

A.B.C.D.

Answer 1

【答案】D

【解析】

延长AD交⊙O于R，连接BI，BR，易证△BRI为等腰直角三角形，OI为△ABR的中位线，设OI＝a，则BR＝2a＝IR＝AI，则OA＝a，则sin∠CAD＝sin∠OAI＝．

解：如图，

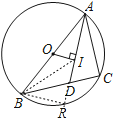
延长AD交⊙O于R，连接BI，BR，

∵I为△ABC的内心，

∴∠CAR＝∠BAR，∠ABI＝∠CBI，

∵∠CAR＝∠CBR，

∴∠RIB＝∠IAB+∠IBA＝∠CAR+∠CBI＝∠CBR+∠CBI＝∠RBI，

∴RB＝BI，

∵AB是⊙O的直径，

∴∠BRA＝90°，

∴∠△BRI为等腰直角三角形，

∵O是AB中点，OI∥BR，

∴I是AR的中点，

∴OI为△ABR的中位线，

设OI＝a，则BR＝2a＝IR＝AI，

在Rt△AOI中，根据勾股定理，得

OA＝＝a，

∴sin∠CAD＝sin∠OAI＝＝＝．

所以sin∠CAD的值为．

故选：D．