题目内容
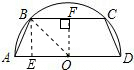
如图，等腰梯形ABCD内接于半圆D，且AB=1，BC=2，则OA=（ ）
A．
| B．
| C．
| D．
|
过点B作BE⊥AD于E，过O作OF⊥CB，连接OB，
∵OF⊥CB，
∴BF=
BC=1，
∴OE=1，
设AE=x，
∵OA、OB是⊙O的半径，
∴OB=OA=x+1，
根据勾股定理，AB2-AE2=OB2-OE2，
得12-x2=（x+1）2-12，
整理，得2x2+2x-1=0，
解得x=
，
故OA=AE+OE=
+1=
．
故选A．
∵OF⊥CB，
∴BF=
| 1 |
| 2 |
∴OE=1，
设AE=x，
∵OA、OB是⊙O的半径，
∴OB=OA=x+1，
根据勾股定理，AB2-AE2=OB2-OE2，
得12-x2=（x+1）2-12，
整理，得2x2+2x-1=0，
解得x=
-1+
| ||
| 2 |
故OA=AE+OE=
-1+
| ||
| 2 |
1+
| ||
| 2 |
故选A．
练习册系列答案
名校课堂系列答案
相关题目
