Question

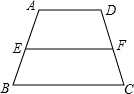
如图，在直角梯形ABCD中，AB∥DC，CB⊥AB，AB=20cm，BC=4cm，CD=15cm．点P、Q分别以A、C同时出发，以v_P=4cm/s，v_Q=1cm/s在AB、CD边上移动，设运动时间为t（s），求：
（1）t为何值时，四边形APQD是平行四边形？
（2）t为何值时，四边形APQD是直角梯形？
（3）t为何值时，四边形APQD是等腰梯形？

Answer 1

∵v_P=4cm/s，v_Q=1cm/s，
∴AP=4t，PB=20-4t，CQ=t，DQ=15-t，
（1）四边形APQD是平行四边形时，AP=DQ，
则4t=15-t，
解得t=3；

（2）四边形APQD是直角梯形时，PB=CQ，
∴20-4t=t，
解得t=4；

（3）如图，过点Q作QE⊥AB于E，过点D作DF⊥AB于F，
则四边形BCDF是矩形，
∴BF=CD=15cm，
∵四边形APQD是等腰梯形，
∴AF=PE，
AF=AB-BF=20-15=5cm，
PE=BF-EF=15-（15-t）=t，
∴t=5．