Ő‚ńŅńŕ»›
°ĺŐ‚ńŅ°Ņő™ŃňŐĹňųīķ ż Ĺ![]() Ķń◊Ó–°÷Ķ£¨
Ķń◊Ó–°÷Ķ£¨
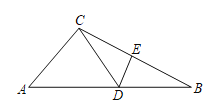
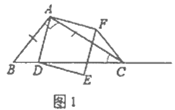
–°’Ň«…√ÓĶń‘ň”√Ńň ż—ßňľŌŽ£ģĺŖŐŚ∑Ĺ∑® «’‚—ýĶń£ļ»ÁÕľ£¨Cő™ŌŖ∂őBD…Ō“Ľ∂ĮĶ„£¨∑÷ĪūĻżĶ„B°ĘD◊ų![]() £¨Ń¨ĹŠAC°ĘEC£ģ“—÷™AB=1£¨DE=5£¨BD=8£¨…ŤBC=x£ģ‘Ú
£¨Ń¨ĹŠAC°ĘEC£ģ“—÷™AB=1£¨DE=5£¨BD=8£¨…ŤBC=x£ģ‘Ú![]() £¨
£¨![]() ‘Úő Ő‚ľī◊™ĽĮ≥…«ůAC+CEĶń◊Ó–°÷Ķ£ģ
‘Úő Ő‚ľī◊™ĽĮ≥…«ůAC+CEĶń◊Ó–°÷Ķ£ģ
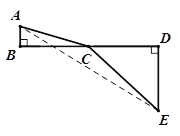
(1)ő“√«÷™ĶņĶĪA°ĘC°ĘE‘ŕÕ¨“Ľ÷ĪŌŖ…Ō Ī£¨AC+CEĶń÷Ķ◊Ó–°£¨”ŕ «Ņ…«ůĶ√![]() Ķń◊Ó–°÷ĶĶ»”ŕ £¨īň Īx= £Ľ
Ķń◊Ó–°÷ĶĶ»”ŕ £¨īň Īx= £Ľ
(2)Ő‚÷–°į–°’Ň«…√ÓĶń‘ň”√Ńň ż—ßňľŌŽ°Ī «÷łńń÷÷÷ų“™Ķń ż—ßňľŌŽ£Ľ
(—°ŐÓ£ļļĮ żňľŌŽ£¨∑÷ņŗŐ÷¬ŘňľŌŽ°ĘņŗĪ»ňľŌŽ°Ę ż–őĹŠļŌňľŌŽ)
(3)«Žń„łýĺ›…Ō ŲĶń∑Ĺ∑®ļÕĹŠ¬Ř£¨ ‘ĻĻÕľ«ů≥Ųīķ ż Ĺ![]() Ķń◊Ó–°÷Ķ£ģ
Ķń◊Ó–°÷Ķ£ģ
°ĺīūįł°Ņ£®1£©10£¨![]() £Ľ£®2£© ż–őĹŠļŌňľŌŽ£Ľ£®3£©13
£Ľ£®2£© ż–őĹŠļŌňľŌŽ£Ľ£®3£©13
°ĺĹ‚őŲ°Ņ
£®1£©łýĺ›ŃĹĶ„÷ģľšŌŖ∂ő◊Ó∂ŐŅ…÷™AC+CEĶń◊Ó–°÷ĶĺÕ «ŌŖ∂őAEĶń≥§∂»£ģĻżĶ„E◊ųEF°őBD£¨ĹĽABĶń—”≥§ŌŖ”ŕFĶ„£ģ‘ŕRt°ųAEF÷–‘ň”√ĻīĻ…∂®ņŪľ∆ň„«ůĹ‚£Ľ
£®2£©–°’Ň«…√ÓĶń‘ň”√Ńň ż–őĹŠļŌňľŌŽ£Ľ
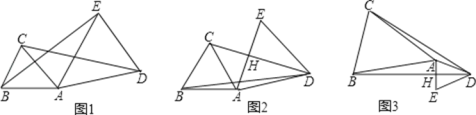
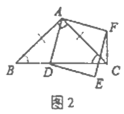
£®3£©”…£®1£©ĶńĹŠĻŻŅ…◊ųBD=12£¨ĻżĶ„A◊ųAF°őBD£¨ĹĽDEĶń—”≥§ŌŖ”ŕFĶ„£¨ ĻAB=2£¨ED=3£¨Ń¨Ĺ”AEĹĽBD”ŕĶ„C£¨»ĽļůĻĻ‘žĺō–őAFDB£¨Rt°ųAFE£¨ņŻ”√ĺō–őĶń÷ĪĹ«»żĹ«–őĶń–‘÷ Ņ…«ůĶ√AEĶń÷ĶĺÕ «īķ ż Ĺ![]() Ķń◊Ó–°÷Ķ£ģ
Ķń◊Ó–°÷Ķ£ģ
Ĺ‚£ļ£®1£©ĻżĶ„E◊ųEF°őBD£¨ĹĽABĶń—”≥§ŌŖ”ŕFĶ„

łýĺ›Ő‚“‚£¨ňńĪŖ–őBDEFő™ĺō–ő
AF=AB+BF=5+1=6£¨EF=BD=8
°ŗ![]()
ľīAC+CEĶń◊Ó–°÷Ķ «10
![]()
°ŖEF°őBD
°ŗ![]()
°ŗ![]()
Ĺ‚Ķ√£ļ![]()
Ļ īūįłő™£ļ10£Ľ![]() £Ľ
£Ľ
£®2£©–°’Ň«…√ÓĶń‘ň”√Ńň ż–őĹŠļŌňľŌŽ£Ľ
£®3£©ĻżĶ„A◊ųAF°őBD£¨ĹĽDEĶń—”≥§ŌŖ”ŕFĶ„

łýĺ›Ő‚“‚£¨ňńĪŖ–őABDFő™ĺō–ő
EF=AB+DE=2+3=5£¨AF=DB=12
°ŗ![]()
ľīAC+CEĶń◊Ó–°÷Ķ «13£ģ