题目内容
【题目】知识铺垫
通过小学的学习我们知道:
①正方形的四条边都相等,四个角都是直角如在正方形![]() 中,
中,![]() ,
,
![]() .
.
②等腰三角形中相等的两条边所对的两个角也相等。如在![]() 中,如果
中,如果![]() ,那么
,那么![]() .
.
解决问题
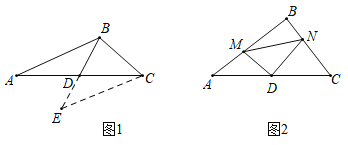
如图1,在![]() 中,
中,![]() 为锐角,点
为锐角,点![]() 为射线
为射线![]() 上一点,连接
上一点,连接![]() ,以
,以![]() 为一边且在
为一边且在![]() 的右侧作正方形
的右侧作正方形![]() ,解答下列问题:
,解答下列问题:
(1)如果![]() ,
,![]()
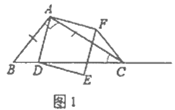
①如图2,当点![]() 在线段
在线段![]() 上时(与点
上时(与点![]() 不重合),线段
不重合),线段![]() 、
、![]() 之间的数量关系为__________,位置关系为__________.
之间的数量关系为__________,位置关系为__________.
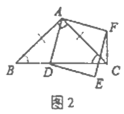
②如图3,当点![]() 在线段
在线段![]() 的延长线上时,①中的结论是否仍然成立,并说明理由.
的延长线上时,①中的结论是否仍然成立,并说明理由.

拓展延伸
(2)如果![]() ,
,![]() .点
.点![]() 在线段
在线段![]() 上,当
上,当![]() __________时,
__________时,![]() (点
(点![]() 、
、![]() 不重合).
不重合).
【答案】(1)①相等,垂直;②成立,理由见解析;(2)45°.
【解析】
(1)①证明△BAD≌△CAF,可得:BD=CF,∠B=∠ACF=45°,则∠BCF=∠ACB+∠ACF=90°,所以BD与CF相等且垂直;
②①的结论仍成立,同理证明△DAB≌△FAC,可得结论:垂直且相等;
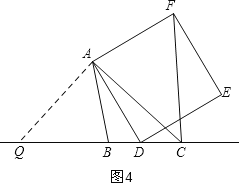
(2)当∠ACB满足45°时,CF⊥BC;如图4,作辅助线,证明△QAD≌△CAF,即可得出结论.
解:(1)①CF与BD数量关系是相等,位置关系是垂直,理由是:
如图2,∵四边形ADEF是正方形,
∴AD=AF,∠DAF=90°,
∴∠DAC+∠CAF=90°,
∵AB=AC,∠BAC=90°,
∴∠BAD+∠DAC=90°,且∠B=∠ACB=45°,
∴∠CAF=∠BAD,
∴△BAD≌△CAF,
∴BD=CF,∠B=∠ACF=45°,
∴∠ACB+∠ACF=45°+45°=90°,
即∠BCF=90°,
∴BC⊥CF,
即BD⊥CF;
故答案为:相等,垂直;
②当点D在BC的延长线上时,①的结论仍成立,理由是:
如图3,由正方形ADEF得AD=AF,∠DAF=90°,
∵∠BAC=90°,
∴∠DAF=∠BAC,
∴∠DAB=∠FAC,
又∵AB=AC,
∴△DAB≌△FAC,
∴CF=BD,
∠ACF=∠ABD,
∵∠BAC=90°,AB=AC,
∴∠ABC=45°,
∴∠ACF=∠ABC=45°
∴∠BCF=∠ACB+∠ACF=90°,
即CF⊥BD;
(2)当∠ACB=45°时,CF⊥BD,理由是:
如图4,过点A作AQ⊥AC,交BC于点Q,
∵∠BCA=45°,
∴∠AQC=45°,
∴∠AQC=∠BCA,
∴AC=AQ,
∵AD=AF,∠QAC=∠DAF=90°,
∴∠QAC-∠DAC=∠DAF-∠DAC,
∴∠QAD=∠CAF,
∴△QAD≌△CAF,
∴∠ACF=∠AQD=45°,
∠BCF=∠ACB+∠ACF=90°,
即CF⊥BD.
故答案为:45°.

 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案