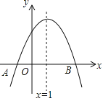题目内容
【题目】已知![]() 中,
中,![]() .
.
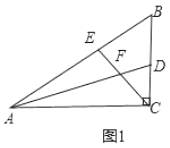
(1)如图1,在![]() 中,若
中,若![]() ,且
,且![]() ,求证:
,求证:![]() ;
;
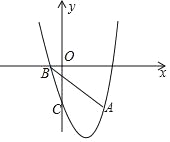
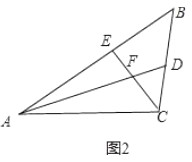
(2)如图2,在![]() 中,若
中,若![]() ,且
,且![]() 垂直平分
垂直平分![]() ,
,![]() ,
,![]() ,求
,求![]() 的长;
的长;
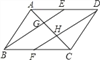
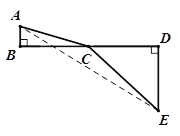
(3)如图3,在![]() 中,当
中,当![]() 垂直平分
垂直平分![]() 于
于![]() ,且
,且![]() 时,试探究
时,试探究![]() ,
,![]() ,
,![]() 之间的数量关系,并证明.
之间的数量关系,并证明.
【答案】(1)证明见解析;(2)5;(3)CD2=BD2+4AH2,证明见解析;
【解析】
(1)求出∠DAC=∠BAE,再利用“边角边”证明△ACD和△ABE全等,再根据全等三角形对应边相等即可得证;
(2)连接BE,先求出△ADE是等边三角形,再根据全等三角形对应边相等可得BE=CD,全等三角形对应角相等可得∠BEA=∠CDA=30°,然后求出∠BED=90°,再利用勾股定理列式进行计算即可得解;
(3)过B作BF⊥BD,且BF=AE,连接DF,先求出四边形ABFE是平行四边形,根据平行四边形对边相等可得AB=EF,设∠AEF=x,∠AED=y,根据平行四边形的邻角互补与等腰三角形的性质求出∠CAD,从而得到∠CAD=∠FED,然后利用“边角边”证明△ACD和△EFD全等,根据全等三角形对应边相等可得CD=DF,然后利用勾股定理列式计算即可得解.
(1)如图1,证明:∵∠DAE=∠BAC,
∴∠DAE+∠CAE=∠BAC+∠CAE,
即∠DAC=∠BAE.
在△ACD与△ABE中,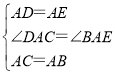 ,
,
∴△ACD≌△ABE(SAS),
∴CD=BE;
(2)如图2,连接BE,
∵CD垂直平分AE
∴AD=DE,
∵∠DAE=60°,
∴△ADE是等边三角形,
∴∠CDA=![]() ∠ADE=
∠ADE=![]() ×60°=30°,
×60°=30°,
∵△ABE≌△ACD,
∴BE=CD=4,∠BEA=∠CDA=30°,
∴BE⊥DE,DE=AD=3,
∴BD=5;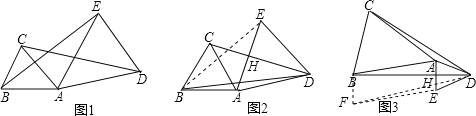
(3)如图3,过B作BF⊥BD,且BF=AE,连接DF,
则四边形ABFE是平行四边形,
∴AB=EF,
设∠AEF=x,∠AED=y,
则∠FED=x+y,
∠BAE=180°-x,∠EAD=∠AED=y,∠BAC=2∠ADB=180°-2y,
∠CAD=360°-∠BAC-∠BAE-∠EAD=360°-(180°-2y)-(180°-x)-y=x+y,
∴∠FED=∠CAD,
在△ACD和△EFD中,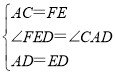 ,
,
∴△ACD≌△EFD(SAS),
∴CD=DF,
而BD2+BF2=DF2,
∴CD2=BD2+4AH2.