Question

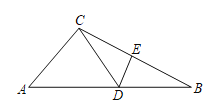
【题目】如图，△ABC中，D为AB上一点，E为BC上一点，且AC=CD=BD=BE=2．

(1)若∠A=40°，求∠CDE；

(2)若图形中所有线段长均为整数，求CE．

Answer 1

【答案】（1）∠CDE=60°；（2）CE=1

【解析】

（1）根据等腰三角形的性质推出∠A=∠CDA=40°，∠B=∠DCB，∠BDE=∠BED，根据三角形的外角性质求出∠B=20°，由三角形的内角和定理求出∠BDE，根据平角的定义即可求出选项；

（2）根据三角形三边关系确定CE的取值范围，再结合图形中所有线段长均为整数即可得解．

（1）∵AC=CD=BD=BE，∠A=40°

∴∠A=∠CDA=40°，∠B=∠DCB，∠BDE=∠BED

∵∠B+∠DCB=∠CDA=40°，

∴∠B=20°，

∵∠B+∠EDB+∠DEB=180°，

∴∠BDE=∠BED=（180°﹣20°）=80°，

∴∠CDE=180°﹣∠CDA﹣∠EDB=180°﹣40°﹣80°=60°

（2）∵CD=BD=2

∴0＜BC＜4

∵BE=2

∴0＜CE＜2

∵图形中所有线段长均为整数

∴CE=1．