题目内容
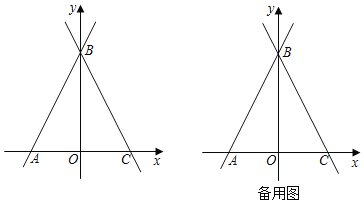
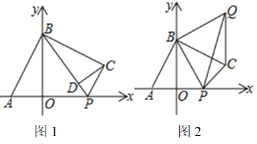
【题目】已知:如图,在平面直角坐标系中,A(a,0)、B(0,b),且|a+2|+(b+2a)2=0,点P为x轴上一动点,连接BP,在第一象限内作BC⊥AB且BC=AB
(1) 求点A、B的坐标
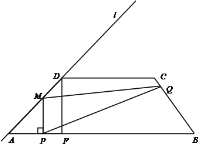
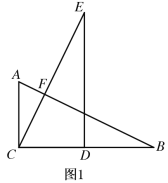
(2) 如图1,连接CP.当CP⊥BC时,作CD⊥BP于点D,求线段CD的长度
(3) 如图2,在第一象限内作BQ⊥BP且BQ=BP,连接PQ.设P(p,0),直接写出S△PCQ=_____
【答案】(1)A(-2,0),B(0,4);(2)CD=2;(3)![]()
【解析】
(1)由非负数的性质,可求出a、b的值,得到A、B的坐标;
(2)过C作CE⊥OB于E,与PB交于F,易证△AOB≌△BEC,可得OA=BE=2,即E为OB中点,所以EF为△BOP的中位线,F为Rt△BCP斜边BP上的中点,所以![]() ,所以∠BCF=∠CBD=∠ABO,再证△AOB≌△CDB即可得CD=OA.
,所以∠BCF=∠CBD=∠ABO,再证△AOB≌△CDB即可得CD=OA.
(3)过B作BG⊥CQ于点G,延长QC与x轴交于H,通过证△ABP≌△CBQ,△BOP≌△BGQ可推出OBGH为矩形,以CQ为底,PH为高求面积.
解:(1)∵|a+2|+(b+2a)2=0
∴a+2=0,b+2a=0,解得a=-2,b=4,
∴A(-2,0),B(0,4)
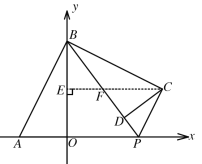
(2)如图所示,过C作CE⊥OB于E,与PB交于F,
∵BC⊥AB,∴∠ABO+∠EBC=90°,
在Rt△BCE中,∠EBC+∠BCE=90°,
∴∠ABO=∠BCE
在△AOB和△BEC中,
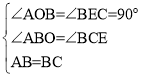
∴△AOB≌△BEC(AAS)
∴BE=AO=2,又∵OB=4,∴E为OB的中点,
∵EC∥OP,∴EF为△BOP的中位线,则F为BP的中点,
在Rt△BCP中,CF为斜边上的中线,
∴![]()
∴∠BCE=∠CBD=∠ABO
在△AOB和△CDB中
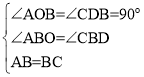
∴△AOB≌△CDB(AAS)
∴CD=AO=2
(3)如下图所示,过B作BG⊥CQ于点G,延长QC与x轴交于H,

∵∠ABP+∠PBC=90°,∠PBC+CBQ=90°,
∴∠ABP=∠CBQ
在△ABP与△CBQ中,
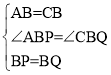
∴△ABP≌△CBQ(SAS)
∴∠BPO=∠BQG,CQ=AP=2+p,
在△BOP和△BGQ中,
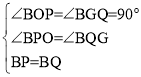
∴△BOP≌△BGQ(AAS)
∴∠OBP=∠GBQ,BG=BO=4
又∵∠GBQ+∠PBG=90°
∴∠OBP+∠PBG=90°,即∠OBG=90°,
在四边形OBGH中,∠OBG=∠BOG=∠BGH=90°,
∴∠OHG=90°,∴PH是△PCQ中CQ边上的高,
PH=OH-OP=4-p
∴![]()

 一线名师提优试卷系列答案
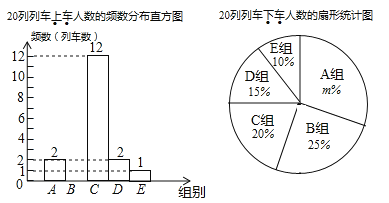
一线名师提优试卷系列答案【题目】根据重庆轨道集团提供的日客运量统计,2019年2月21日重庆轨道交通首次日客运量突破300万乘次,其中近期开通的重庆轨道交通环线日客运量为21.5万乘次.据了解,某工作日上午7点至9点轨道环线四公里站有20列列车进出站,每列车进出站时,将上车和下车的人数记录下来,各得到20个数据,并将数据进行整理,绘制成了如下两幅不完整统计图.(数据分组为:![]() 组:
组:![]() ,
,![]() 组:
组:![]() ,
,![]() 组:
组:![]() ,
,![]() 组:
组:![]() ,
,![]() 组:
组:![]() )
)
I.上车人数在![]() 组的是:190,190,191,192,193,193,195,196,198,198,198,198;
组的是:190,190,191,192,193,193,195,196,198,198,198,198;
II.上车人数的平均数、中位数如下表:
平均数 | 中位数 | |
上车人数(人) | 194 | a |
根据以上信息,回答下列问题:
(1)请补全频数分布直方图;
(2)表中![]() ________,扇形统计图中
________,扇形统计图中![]() _________,扇形统计图中
_________,扇形统计图中![]() 组所在的圆心角度数为________度;
组所在的圆心角度数为________度;
(3)请利用平均数,估算一周内5个工作日的上午7点至9点重庆轨道环线四公里站的上车总人数.