Question

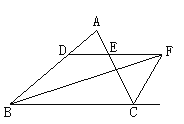
【题目】如图，点B在线段AC上，点E在线段BD上，∠ABD=∠DBC，AB=DB，EB=CB，M，N分别是AE，CD的中点。试探索BM和BN的关系，并证明你的结论。

Answer 1

【答案】BM⊥BN．见解析

【解析】试题分析：根据SAS推出△ABE≌△DBC，推出AE=DC，∠EAB=∠BDC，∠AEB=∠DCB，求出∠ABD=∠DBC=90°，BM=AM=EM=AE，BN=CN=DN=CD，推出∠ABM=∠DBN，∠EBM=∠NBC即可．

解：BM=BN，BM⊥BN，

理由是：在△ABE和△DBC中，

，

∴△ABE≌△DBC（SAS），

∴AE=DC，∠EAB=∠BDC，∠AEB=∠DCB，

∵∠ABD=∠DBC，∠ABD+∠DBC=180°，

∴∠ABD=∠DBC=90°，

∵M为AE的中点，N为CD的中点，

∴BM=AM=EM=AE，BN=CN=DN=CD，

∴BM=BN，∠EAB=∠MBA，∠CDB=∠DBN，∠AEB=∠EBM，∠NCB=∠NBC，

∵∠EAB=∠BDC，∠AEB=∠DCB，

∴∠ABM=∠DBN，∠EBM=∠NBC，

∴∠ABC=2∠DBN+2∠EBM=180°，

∴∠EBN+∠EBM=90°，

∴BM⊥BN．