题目内容
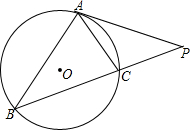
如图1,已知O是锐角∠XAY的边AX上的动点,以点O为圆心、R为半径的圆与射线AY切于点B,交射线OX于点C,连接BC,作CD⊥BC ,交AY于点D.
,交AY于点D.
(1)求证:△ABC∽△ACD;
(2)若P是AY上一点,AP=4,且sinA=
,
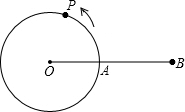
①如图2,当点D与点P重合时,求R的值;
②当点D与点P不重合时,试求PD的长(用R表示).
 ,交AY于点D.
,交AY于点D.(1)求证:△ABC∽△ACD;
(2)若P是AY上一点,AP=4,且sinA=
| 3 |
| 5 |
①如图2,当点D与点P重合时,求R的值;
②当点D与点P不重合时,试求PD的长(用R表示).
(1)证明:由已知,CD⊥BC,
∴∠ADC=90°-∠CBD.
又∵⊙O切AY于点B,
∴OB⊥AB.
∴∠OBC=90°-∠CBD.
∴∠ADC=∠OBC.
又在⊙O中,OB=OC=R,
∴∠OBC=∠ACB.
∴∠ACB=∠ADC.
又∠A=∠A,
∴△ABC∽△ACD.
(2)由已知,sinA=
,
又OB=OC=R,OB⊥AB,
∴在Rt△AOB中,AO=
=
=
R,AB=
=
R.
∴AC=
R+R=
R.
由(1)已证,△ABC∽△ACD,
∴
=
.
∴
=
.
因此AD=
R.
①当点D与点P重合时,AD=AP=4,
∴
R=4.
∴R=
.
②当点D与点P不重合时,有以下两种可能:
(i)若点D在线段AP上(即0<R<
),PD=AP-AD=4-
R,
(ii)若点D在射线PY上(即R>
),PD=AD-AP=
R-4,
综上,当点D在线段AP上(即0<R<
)时,PD=4-
R,
当点D在射线PY上(即R>
)时,PD=
R-4,
又当点D与点P重合(即R=
)时,PD=0,故在题设条件下,总有PD=|
R-4|(R>0).
∴∠ADC=90°-∠CBD.
又∵⊙O切AY于点B,
∴OB⊥AB.
∴∠OBC=90°-∠CBD.
∴∠ADC=∠OBC.
又在⊙O中,OB=OC=R,
∴∠OBC=∠ACB.
∴∠ACB=∠ADC.
又∠A=∠A,
∴△ABC∽△ACD.
(2)由已知,sinA=
| 3 |
| 5 |
又OB=OC=R,OB⊥AB,
∴在Rt△AOB中,AO=
| OB |
| sinA |
| R | ||
|
| 5 |
| 3 |
(
|
| 4 |
| 3 |
∴AC=
| 5 |
| 3 |
| 8 |
| 3 |
由(1)已证,△ABC∽△ACD,
∴
| AC |
| AB |
| AD |
| AC |
∴
| ||
|
| AD | ||
|
因此AD=
| 16 |
| 3 |
①当点D与点P重合时,AD=AP=4,
∴
| 16 |
| 3 |
∴R=
| 3 |
| 4 |
②当点D与点P不重合时,有以下两种可能:
(i)若点D在线段AP上(即0<R<
| 3 |
| 4 |
| 16 |
| 3 |
(ii)若点D在射线PY上(即R>
| 3 |
| 4 |
| 16 |
| 3 |
综上,当点D在线段AP上(即0<R<
| 3 |
| 4 |
| 16 |
| 3 |
当点D在射线PY上(即R>
| 3 |
| 4 |
| 16 |
| 3 |
又当点D与点P重合(即R=
| 3 |
| 4 |
| 16 |
| 3 |

练习册系列答案
 学习实践园地系列答案
学习实践园地系列答案
相关题目