��Ŀ����
����Ŀ��ͨ���ⷽ�̣��飩ʹ����õ������˼ά��ʽ���Ƿ���˼�룬��ѧ���ġ����ɶ���������һ�κ����������������е���ϵ��������̼���ġ�һԪ���η��̡�����Ҳѧϰ��������ⷽ����Ӧ�á���ͼ1������![]() �У�
��![]() ��
��![]() �ϣ���
�ϣ���![]() ����
����![]() �ӵ�
�ӵ�![]() ��������1����λÿ����ٶ���
��������1����λÿ����ٶ���![]() �������
�������![]() �˶������
�˶������![]() ���˶�ʱ��Ϊ
���˶�ʱ��Ϊ![]() �롣
�롣
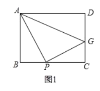
��1��![]() �����Ϊ
�����Ϊ![]() ����
����![]() ����
����![]() �ĺ�����ϵʽ�������
�ĺ�����ϵʽ�������![]() ʱ
ʱ![]() ��ֵ��
��ֵ��
��2���ڵ�![]() �ӵ�
�ӵ�![]() ��
��![]() �˶��Ĺ����У��Ƿ����ʹ
�˶��Ĺ����У��Ƿ����ʹ![]() ��ʱ�̣������ڣ����
��ʱ�̣������ڣ����![]() ��ֵ���������ڣ���˵�����ɣ�
��ֵ���������ڣ���˵�����ɣ�
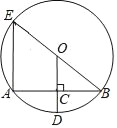
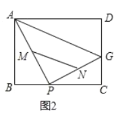
��3����ͼ2��![]() �ֱ���
�ֱ���![]() ���е㣬�ڵ�
���е㣬�ڵ�![]() ��
��![]() ��
��![]() �˶��Ĺ����У��߶�
�˶��Ĺ����У��߶�![]() ɨ����ͼ����ʲô��״_________________����ֱ��д���������___________________________��
ɨ����ͼ����ʲô��״_________________����ֱ��д���������___________________________��
���𰸡���1��x=8����2�����ڣ�x=6����3��ƽ���ı��Σ�15.
��������
��1��![]() ��
��![]() ��Ȼ������
��Ȼ������![]() �����
�����![]() ������
���ε����![]() ����ֱ�������ε�����ɵõ�
����ֱ�������ε�����ɵõ�![]() ��
��![]() �ĺ�����ϵʽ��Ȼ��
�ĺ�����ϵʽ��Ȼ��![]() ���뺯����ϵʽ�����
���뺯����ϵʽ�����![]() ��ֵ��
��ֵ��
��2�������ݹ��ɶ������![]() ��
��![]() ��
��![]() �ij���Ȼ�����ݹ��ɶ������涨���г�����
�ij���Ȼ�����ݹ��ɶ������涨���г�����![]() �ķ��̣��Ӷ������
�ķ��̣��Ӷ������![]() ��ֵ��
��ֵ��
��3��ȷ������![]() �ֱ����
�ֱ����![]() �͵�
�͵�![]() �غ�ʱ����
�غ�ʱ����![]() ��
��![]() ��λ�ã�Ȼ�����������ε���λ�߶�����֤��
��λ�ã�Ȼ�����������ε���λ�߶�����֤��![]() ��
��![]() ���Ӷ����жϳ�
���Ӷ����жϳ�![]() ɨ���������״��Ȼ������ƽ���ı��ε������ʽ��⼴�ɣ�
ɨ���������״��Ȼ������ƽ���ı��ε������ʽ��⼴�ɣ�
�⣺��1��![]() �ı���
�ı���![]() Ϊ���Σ�
����
![]() ��
��![]() ��
��
![]() ��
��
![]() ��
��
![]() ��
��![]() ��
��
![]() ��
��
�����ã�![]() ��
��
��![]() ʱ��
ʱ��![]() ��
��
��ã�![]() ��
��
��2�����ڣ��������£�
![]() ��
��![]() ��
��![]() ��
��![]() ��
��
![]() ��
��![]() ��
��![]() ��
��
![]() ��
��![]() ʱ��
ʱ��![]() ��
��
![]() ��
��
�����ã�![]() ��
��
�䷽�ã�![]() ��
��
��ã�![]() ��
��
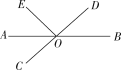
��3����ͼ��ʾ��
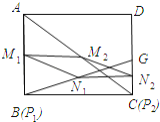
![]() ����
����![]() ���
���![]() �غ�ʱ����
�غ�ʱ����![]() λ��
�![]() ������
������![]() λ�ڵ�
λ�ڵ�![]() ����
����
![]() Ϊ
Ϊ![]() ���е㣬��
���е㣬��![]() λ
λ![]() ���е㣮
���е㣮
![]() ����
����![]() ���
���![]() �غ�ʱ����
�غ�ʱ����![]() λ��
�![]() ������
������![]() λ�ڵ�
λ�ڵ�![]() ����
����
![]() Ϊ
Ϊ![]() ���е㣬��
���е㣬��![]() λ
λ![]() ���е㣮
���е㣮
![]() ��
��![]() ��
��![]() ��
��![]() ��
��
![]() ��
��![]() ��
��
![]() �ı���
�ı���![]() Ϊƽ���ı��Σ�
Ϊƽ���ı��Σ�
![]() ɨ��������Ϊƽ���ı��Σ�
ɨ��������Ϊƽ���ı��Σ�
![]()
�ʴ�Ϊ��ƽ���ı��Σ�15��

����Ŀ��ijʯ����ϩ��ij���������ס����������ϵ������Ϣ���±����������������⣺
������ | �ɱ��� | ���۴����� | |
�������� | 2100��Ԫ/�֣� | 800��Ԫ/�֣� | 200��Ԫ/�֣� |
�������� | 2400��Ԫ/�֣� | 1100��Ԫ/�֣� | 100��Ԫ/�֣� ��ÿ�»���֧���豸������ά����20000Ԫ |
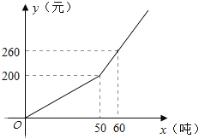
��1����ó���ÿ�������ס����������ϸ�x�֣�����ֱ�Ϊy1Ԫ��y2Ԫ���ֱ����y1��y2��x�ĺ�����ϵʽ(ע������=������-��֧��)��
��2����֪�ó���ÿ�������ס����������Ͼ�������400�֣���ij��Ҫ�����ס����������Ϲ�700�֣�����������ס������ϸ����ٶ�ʱ����õ������������������Ƕ��٣�