题目内容
【题目】如图，直线AB，CD相交于点O，OA是∠EOC的平分线，∠EOD＝100°．
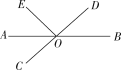
(1)请指出∠BOC的一个补角；
(2)求出∠BOD的度数．
【答案】（1）∠AOC(或∠BOD，∠AOE)；（2）40
【解析】
（1）根据补角定义可得∠AOC，∠BOD，∠AOE都是∠BOC的补角；
（2）根据“同角的补角相等”得∠BOD＝∠AOC，再根据平角的定义和角平分线的定义即可得到∠BOD的度数．
(1)∠BOC的补角为∠AOC(或∠BOD，∠AOE)．
(2)根据“同角的补角相等”，得∠BOD＝∠AOC．
因为∠EOD＝100°，∠EOD＋∠EOC＝180°，
所以∠EOC＝180°－∠EOD＝180°－100°＝80°．
因为OA是∠EOC的平分线，所以∠AOC＝
∠EOC＝40°．
所以∠BOD＝40°．
练习册系列答案
53天天练系列答案
相关题目
【题目】为了解黔东南州某县2013届中考学生的体育考试得分情况，从该县参加体育考试的4000名学生中随机抽取了100名学生的体育考试成绩作样本分析，得出如下不完整的频数统计表和频数分布直方图．
成绩分组 | 组中值 | 频数 |
25≤x＜30 | 27.5 | 4 |
30≤x＜35 | 32.5 | m |
35≤x＜40 | 37.5 | 24 |
40≤x＜45 | a | 36 |
45≤x＜50 | 47.5 | n |
50≤x＜55 | 52.5 | 4 |
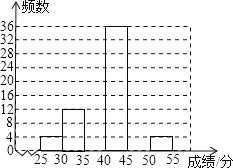
（1）求a、m、n的值，并补全频数分布直方图；
（2）若体育得分在40分以上（包括40分）为优秀，请问该县中考体育成绩优秀学生人数约为多少？
