题目内容
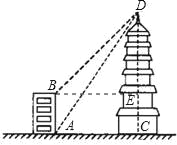
【题目】如图，大楼AB的高为16m，远处有一塔CD，小李在楼底A处测得塔顶D处的仰角为 60°，在楼顶B处测得塔顶D处的仰角为45°，其中A、C两点分别位于B、D两点正下方，且A、C两点在同一水平线上，求塔CD的高．（
=1.73，结果保留一位小数．）
【答案】塔CD的高度为37.9米
【解析】试题分析：首先分析图形，根据题意构造直角三角形．本题涉及两个直角三角形，即Rt△BED和Rt△DAC，利用已知角的正切分别计算，可得到一个关于AC的方程，从而求出DC．
试题解析：作BE⊥CD于E．
可得Rt△BED和矩形ACEB．
则有CE=AB=16，AC=BE．
在Rt△BED中，∠DBE=45°，DE=BE=AC．
在Rt△DAC中，∠DAC=60°，DC=ACtan60°=
AC．
∵16+DE=DC，
∴16+AC=
AC，
解得：AC=8
+8=DE．
所以塔CD的高度为（8
+24）米≈37.9米，
答：塔CD的高度为37.9米．
练习册系列答案
相关题目
