题目内容
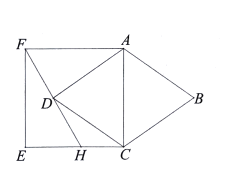
【题目】如图,在![]() 中,
中,![]() (圆心
(圆心![]() 在
在![]() 内部)经过
内部)经过![]() 两点,交线段
两点,交线段![]() 于点
于点![]() 直径
直径![]() 交
交![]() 于点
于点![]() 点
点![]() 关于直线
关于直线![]() 的对称点
的对称点![]() 落在
落在![]() 上.连结
上.连结![]() .
.
![]() 求证:
求证:![]() .
.
![]() 在圆心
在圆心![]() 的运动过程中,
的运动过程中,
![]() 若
若![]() ,求
,求![]() 的长.
的长.
![]() 若点
若点![]() 关于
关于![]() 的对称点落在
的对称点落在![]() 边上时,求
边上时,求![]() 的值.(直接写出答案)
的值.(直接写出答案)
![]() 令
令![]() 与边
与边![]() 的另一个交点为
的另一个交点为![]() ,连结
,连结![]() 交
交![]() 于点
于点![]() 若
若![]() ,垂足为点
,垂足为点![]() 求证:
求证:![]() .
.
【答案】(1)证明见解析;(2)①![]() ;②
;②![]() 或
或![]() ;(3)证明见解析.
;(3)证明见解析.
【解析】
(1)由对称的性质可得∠A=∠BFD,结合∠BFD=∠C,即可推出结论;
(2)①先证∠DFE为直角,设![]() ,再用含a的代数式分别将FE,DE,EC表示出来,根据
,再用含a的代数式分别将FE,DE,EC表示出来,根据![]() 列方程即可求出CE的长;
列方程即可求出CE的长;
②分两种情况讨论,当点F关于AC的对称点落在BF边上时,连接DO,设FF'交AC于点M,证明BD=BE,△BOD是等腰直角三角形,即可求出结果;当点F关于AC的对称点落在BE边上时,点F'与点O重合,证明△DOF为等边三角形,在Rt△DOE中,利用锐角三角函数即可求出结果;
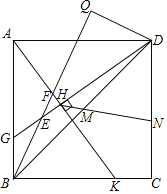
(3)如图作辅助线,先证明△QBG≌△ECM,推出BQ=CE,再证明DQ=DP=AD即可.
解:(1)![]() 点
点![]() 关于直线
关于直线![]() 对称,
对称,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ;
;
(2)①![]() 点
点![]() 关于直线
关于直线![]() 对称,
对称,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() 是直径,
是直径,
![]() 由圆的轴对称性可知:
由圆的轴对称性可知:![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() 设
设![]() ,则
,则![]() ,
,
![]() ,
,
![]() ,
,
解得:![]() ,
,
![]() ;
;
②如图1,当点F关于AC的对称点落在BF边上时,连接DO,设FF'交AC于点M,则AC垂直平分FF',
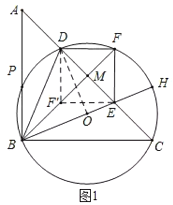
由(1)知,∠A=∠C=45°,∠ABC=90°,
∴BA=BC,∠ABM=∠CBM=45°,
∵点A,F关于直线BD对称,
∴AD=DF,AB=FB,
又∵DB=DB,
∴△ABD≌△FBD(SSS),
∴∠ABD=∠FBD,
∵△BFE≌△BCE,
∴∠FBE=∠CBE,
∴∠ABD=∠FBD=∠FBE=∠CBE=22.5°,
∴∠DBE=∠DBF+∠EBF=45°,
∵OD=OB,
∴∠OBD=∠ODB=45°,
∴∠DOB=90°,
在△BDM与△BEM中,∠BDM=∠BEM=90°22.5°=67.5°,
∴BD=BE,
在等腰Rt△BOD中,设OB=OD=r,则BD=![]() ,
,
∴BE=![]() ,OE=
,OE=![]() ,
,
∴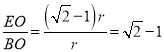 ;
;
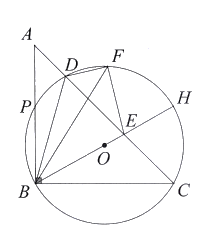
如图2,当点F关于AC的对称点落在BE边上时,
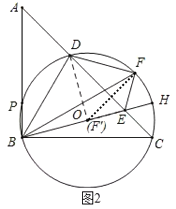
∵∠DF'E=∠DFE=90°,∠DOB=90°
∴点F'与点O重合,
连接OF,则OD=OF=DF,
∴△DOF为等边三角形,
∴∠ODF=60°,
∴∠ODE=∠FDE=30°,
在Rt△DOE中,tan∠ODE=![]() =tan30°=
=tan30°=![]() ,
,
∴![]() ,
,
综上所述,![]() 的值为
的值为![]() 或
或![]() ;
;
(3)连结![]() ;FC交
;FC交![]() 于点
于点![]() ,
,
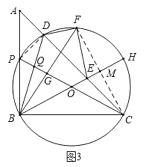
![]() ,
,
∴PC是直径,
∵![]() ,
,
![]() ,
,
![]() 是等边三角形,
是等边三角形,
![]() ,
,
∵![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
∴![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.